E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02785, n°G1SPHCH02795 et n°G1SPHCH02802
Télécharger l’exercice en PDF :
I. Synthèse de l’éthanoate de benzyle au laboratoire
Le jasmin est un arbuste originaire d’Inde, très cultivé dans les régions chaudes. L’odeur de fleur de jasmin correspond à la combinaison de plusieurs espèces chimiques et entre dans la composition de nombreux parfums. L’une des espèces responsables de la senteur du jasmin est l’éthanoate de benzyle. Cet ester est préparé par action de l’acide éthanoïque sur l’alcool benzylique ; cette transformation est non totale, lente et un catalyseur, l’acide sulfurique, est ajouté pour la rendre plus rapide.
Données :
- Propriétés physico-chimiques des espèces mises en jeu :
| Espèces chimiques | Alcool benzylique | Acide éthanoïque | Éthanoate de benzyle | Eau salée saturée |
| Formule brute | C7H8O | C2H4O2 | C9H10O2 | |
| Masse molaire (g.mol-1) | 108,0 | 60,0 | 150,0 | |
| Masse volumique (g.mL-1) | 1,05 | 1,05 | 1,06 | 1,20 |
| Solubilité dans l’eau | Faible | très grande | très faible | |
| Solubilité dans l’eau salée | plus faible que dans l’eau | très grande | insoluble |
Protocole de synthèse mis en œuvre :
a. Sous la hotte, muni de gants et de lunettes, introduire 15 mL d’acide éthanoïque, 12 mL d’alcool benzylique, quelques gouttes d’acide sulfurique concentré et quelques grains de pierre ponce dans un ballon. Chauffer à reflux ce mélange pendant 30 minutes. Laisser refroidir.
b. Introduire dans l’ampoule à décanter le mélange réactionnel et 50 mL d’une solution saturée de chlorure de sodium. Agiter puis laisser décanter. Récupérer la phase qui contient l’éthanoate de benzyle (phase organique).
c. Sécher la phase organique en y ajoutant quelques cristaux de sulfate de magnésium anhydre.
d. Vérifier la pureté du produit obtenu par spectroscopie infrarouge.
1. Nommer chacune des 4 étapes du protocole notées de a à d.
a : transformation des réactifs
b : isolement
c : purification
d : analyse
2. Quel est l’intérêt du montage à reflux?
Le chauffage à reflux permet d’accélérer la réaction, sans perte de matière.
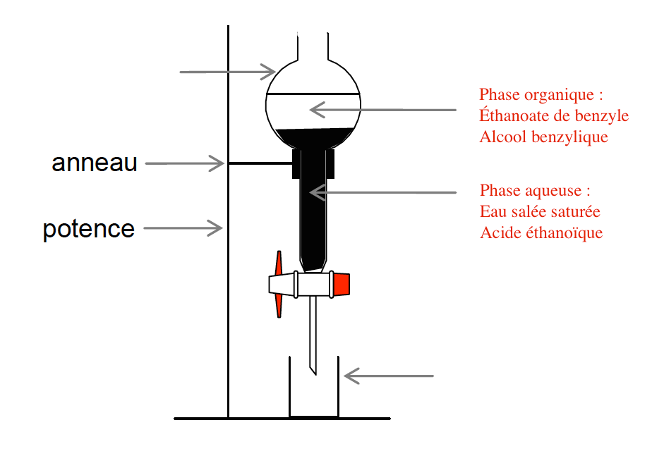
3. Schématiser et légender l’ampoule à décanter après décantation, en précisant la composition de chaque phase. Justifier la position relative des phases.
D’après le texte introductif, cette transformation est non totale, c’est pourquoi il reste des réactifs en fin de réaction.
L’acide éthanoïque est soluble dans l’eau salée, c’est pourquoi il s’y trouve.
L’éthanoate de benzyle est insoluble dans l’eau salée et l’alcool benzylique est très peu soluble dans l’eau salée, c’est pourquoi ils constituent la phase organique.
La masse volumique de l’eau salée est supérieure à celle de l’éthanoate de benzyle, c’est pourquoi elle est en dessous.
4. Écrire l’équation de la réaction modélisant la synthèse de l’éthanoate de benzyle sachant qu’il se forme également de l’eau.
C7H8O + C2H4O2 → C9H10O2+H2O
5. On obtient 6,0 g d’éthanoate de benzyle analysé comme pur. Déterminer la valeur du rendement de la synthèse. Commenter cette valeur.
Calculons les quantités de matières initiales des réactifs
$n=\frac{m}{M}$ et $\rho=\frac{m}{V}$
ainsi $n=\frac{\rho\times V}{M}$
Pour l’alcool benzylique
$n_{ab}=\frac{\rho_{ab}\times V_{ab}}{M_{ab}}=\frac{1,05\times12}{108,0}=0,12\ mol$
Pour l’acide éthanoïque :
$n_{ae}=\frac{\rho_{ae}\times V_{ae}}{M_{ae}}=\frac{1,05\times15}{60,0}=0,26\ mol$
Calculons la quantité de matières finale de l’éthanoate de benzyle :
$n=\frac{m}{M}=\frac{6,0}{150}=4,0.10^{-2}\ mol$
| Équation | C7H8O | + C2H4O2 | → C9H10O2 | +H2O | |
| État initial | x=0mol | 0,12 | 0,26 | 0 | 0 |
| État intermédiaire | x | 0,12-x | 0,26-x | x | x |
| État final | x=xf | 0,12- xf | 0,26- xf | xf | xf |
Calculons $x_{max}$ :
$0,12 – x_{max1} = 0$ $x_{max1} = 0,12\ mol$
$0,26 – x_{max2} = 0$ $x_{max2} = 0,26\ mol$
Donc $x_{max} = 0,12\ mol$
Calculons la masse théorique de l’éthanoate de benzyle :
$n=\frac{m}{M}$
$m = n\times M = x_{max}\times M = 0,12\times150 = 18\ g$
Calculons le rendement :
$r=\frac{m_{exp}}{m_{th}}=\frac{6,0}{18}=33%$
II. Système de convoyage pour les médicaments
Dans une pharmacie, afin d’optimiser la durée de délivrance des médicaments, un toboggan est installé entre le premier étage et le rez-de-chaussée. Un robot combiné à un automate dispose le médicament sur un tapis roulant, en fonction des commandes. Le pharmacien réceptionne le produit à l’étage inférieur pour le donner au client. Le schéma du dispositif est représenté ci-dessous.
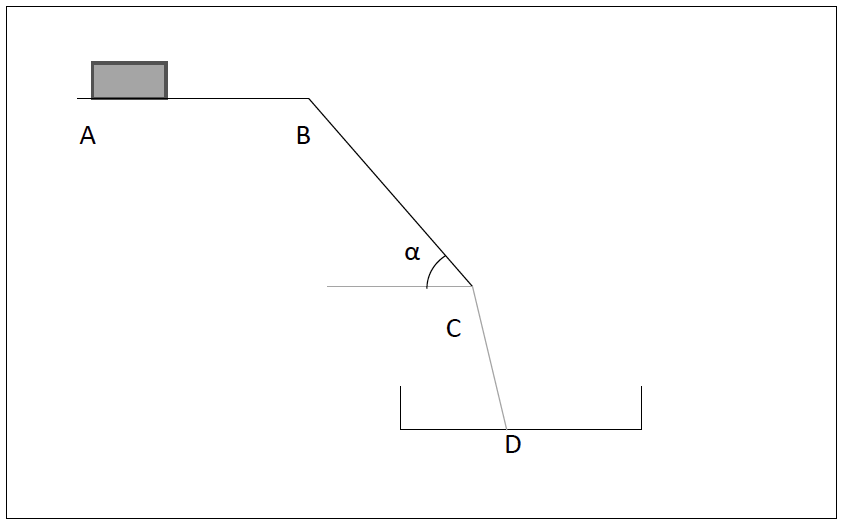
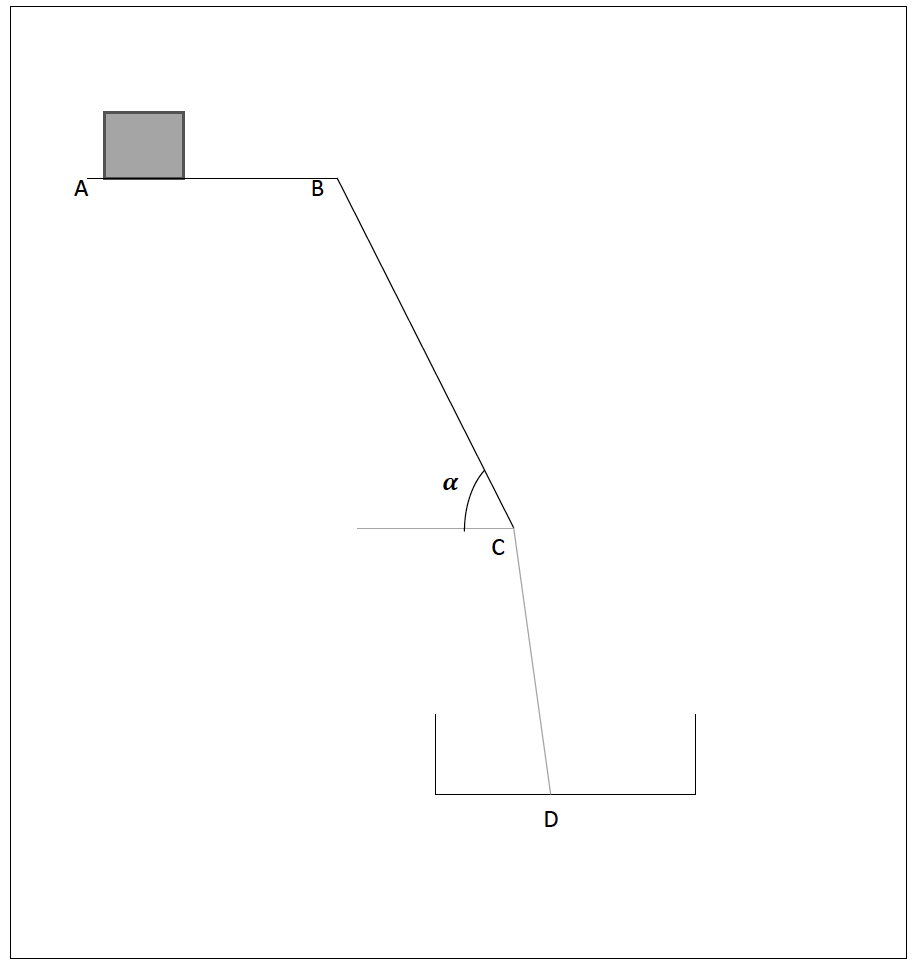
On considère une boîte de médicament de masse 300 g placée sur un tapis. Elle est modélisée par un point matériel de centre d’inertie G. Le trajet parcouru par la boîte est divisé en 3 parties :
- une surface horizontale AB. Il s’agit d’un tapis roulant permettant de faire avancer la boîte de médicament à une vitesse constante v0= 0,3 m.s-1 ;
- Un plan incliné BC de longueur 1,58 m et formant un angle 𝜶 = 55°avec l’horizontale. La valeur de la force F modélisant les frottements exercés sur la boîte de médicaments sur cette portion est F = 0,30N ;
- Une portion de C à D où la boîte est en chute libre, dans un panier au point D.
On néglige l’action exercée par l’air. L’intensité du champ de pesanteur terrestre vaut g = 9,81 N.kg-1.
6. Effectuer le bilan des actions modélisées par des forces s’exerçant sur la boîte de médicaments sur les différents trajets entre A et D.
Sur AB : le poids et la réaction du support
Sur BC : le poids, la réaction du support et la force de frottements
Sur CD : le poids (car chute libre)
7. Que peut-on dire des forces s’exerçant sur la boîte entre les points A et B ?
Sur AB le mouvement est rectiligne uniforme.
D’après la réciproque de la 1ère loi de Newton : $\sum \overrightarrow{F}=\overrightarrow{0}$
8. Sur le trajet BC.
8.1. Schématiser, sur l’annexe à rendre avec la copie, les forces qui s’exercent sur la boîte de médicament, sans souci d’échelle.
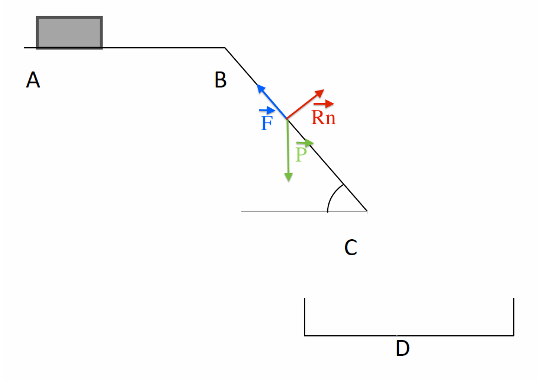
8.2. Donner l’expression littérale du travail de chaque force.
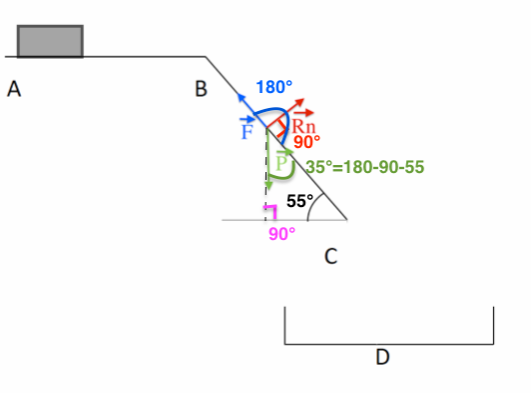
$W_{AB}(\overrightarrow{F})=\overrightarrow{F}\cdot\overrightarrow{AB}=F\times AB\times\cos(\alpha)$
L’angle $\alpha$ est celui entre le vecteur force $\overrightarrow{F}$ et le vecteur déplacement $\overrightarrow{AB}$
$W_{BC}(\overrightarrow{R_n})=\overrightarrow{R_n}\cdot\overrightarrow{BC}=R_n\times BC\times\cos(90^\circ)=0\ J$
$W_{BC}(\overrightarrow{F})=\overrightarrow{F}\cdot\overrightarrow{BC}=F\times BC\times\cos(180^\circ)$
$W_{BC}(\overrightarrow{P})=\overrightarrow{P}\cdot\overrightarrow{BC}=P\times BC\times\cos(35^\circ)$
8.3. En utilisant le théorème de l’énergie cinétique, donner l’expression littérale de la vitesse vC de la boîte de médicaments lorsqu’il arrive en C puis calculer sa valeur.
Théorème de l’énergie cinétique :
$\Delta E_c=\sum W_{AB}(\overrightarrow{F})$
$E_{c(C)}-E_{c(B)}=W_{BC}(\overrightarrow{R_n})+W_{BC}(\overrightarrow{F})+W_{BC}(\overrightarrow{P})$
$\frac{1}{2}m v_C^2-\frac{1}{2}m v_B^2=0+F\times BC\times\cos(180^\circ)+P\times BC\times\cos(35^\circ)$
$\frac{1}{2}m v_C^2=F\times BC\times\cos(180^\circ)+P\times BC\times\cos(35^\circ)+\frac{1}{2}m v_B^2$
$v_C^2=\frac{2}{m}(F\times BC\times\cos(180^\circ)+P\times BC\times\cos(35^\circ)+\frac{1}{2}m v_B^2)$
$v_C^2=\frac{2}{m}\times F\times BC\times\cos(180^\circ)+\frac{2}{m}\times P\times BC\times\cos(35^\circ)+v_B^2$
$v_C=\sqrt{\frac{2}{m}\times BC(F\times\cos(180^\circ)+m\times g\times\cos(35^\circ))+v_0^2}$
$v_C=2,300.10^{-3}\times1,58\times(0,30\times\cos(180^\circ)+300.10^{-3}\times9,81\times\cos(35^\circ))+0,3^2$
$v_C=4,7\ m.s^{-1}$
9. La boîte est réceptionnée dans un panier situé à un hauteur h sous le point C. Indiquer, sans faire de calculs, les paramètres sur lesquels on peut jouer pour que la boîte de médicament ne soit pas déformée à la réception.
Pour que la boîte de médicament ne soit pas déformée à la réception, il faut que son énergie cinétique au point D soit la plus faible possible.
Or entre C et D la boîte est en chute libre. Son énergie mécanique se conserve.
$E_m(D)=E_m(C)$
$E_c(D)+E_p(D)=E_c(C)+E_p(C)$
Or $E_p(D)=0$ donc
$E_c(D)=E_c(C)+E_p(C)$
Ainsi il faut réduire $E_c(C)$ et $E_p(C)$
$E_c(C)=\frac{1}{2}m v_C^2$
Il faut donc diminuer $v_C$ et $m$
$E_p(C)=m\times g\times h$
Il faut donc diminuer $h$ et $m$
En conclusion les paramètres sur lesquels on peut jouer pour que la boîte de médicament ne soit pas déformée à la réception sont $v_C$, $m$ et $h$
Annexe à rendre avec la copie
Question 8.1