Bac Amérique du nord 2023 Sujet 1
Exercice 2 – (5 points) – Durée 0h53 – Calculatrice autorisée
Sujet n°23-PYCJ1AN1
Sujet et corrigé
EXERCICE 2 : TECHNIQUES DE DOSAGE DE L’URÉE (5 POINTS)
En 1773, le pharmacien Hilaire-Marin Rouelle isole de l’urine une substance déchet du métabolisme humain particulièrement riche en azote : l’urée, une molécule de formule brute CH4N2O.
En 1828, le chimiste Friedrich Wöhler synthétise fortuitement pour la première fois de l’urée.
En 1928, le biochimiste Richard Fosse va réaliser le premier dosage précis de l’urée en solution par méthode gravimétrique. Un dosage de l’urée est une indication précieuse de l’état de santé d’une personne. Aujourd’hui, les professionnels des laboratoires d’analyses médicales utilisent une méthode colorimétrique.
D’après Étonnante chimie – Une brève histoire de l’urée : de sa découverte à son dosage, Bernard Bodo,
CNRS EDITIONS et Synthèse de l’urée, André Brack, www.universalis.fr
Cet exercice aborde la synthèse de l’urée et deux techniques de dosage de l’urée en solution. Les différentes parties de cet exercice sont indépendantes.
Données :
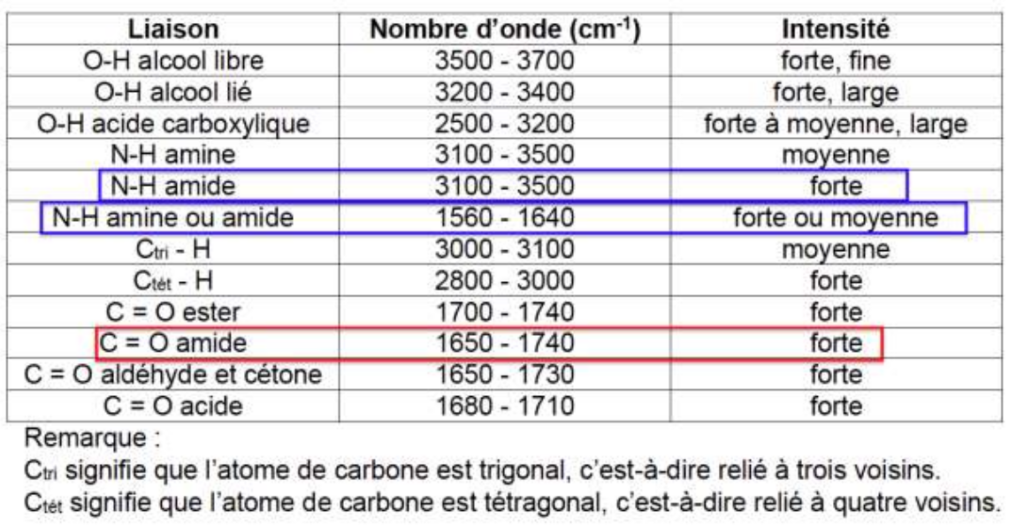
– table spectroscopique IR simplifiée :
| Liaison | Nombre d’onde (cm-1) | Intensité |
| O-H alcool libre | 3500 – 3700 | forte, fine |
| O-H alcool lié | 3200 – 3400 | forte, large |
| O-H acide carboxylique | 2500 – 3200 | forte à moyenne, large |
| N-H amine | 3100 – 3500 | moyenne |
| N-H amide | 3100 – 3500 | forte |
| N-H amine ou amide | 1560 – 1640 | forte ou moyenne |
| Ctri – H | 3000 – 3100 | moyenne |
| Ctét – H | 2800 – 3000 | forte |
| C = O ester | 1700 – 1740 | forte |
| C = O amide | 1650 – 1740 | forte |
| C = O aldéhyde et cétone | 1650 – 1730 | forte |
| C = O acide | 1680 – 1710 | forte |
Remarque :
Ctri signifie que l’atome de carbone est trigonal, c’est-à-dire relié à trois voisins.
Ctét signifie que l’atome de carbone est tétragonal, c’est-à-dire relié à quatre voisins.
– masse molaire moléculaire : M(urée) = 60,06 ± 0,01 g·mol-1 (avec ce qui suit ± correspondant à l’incertitude-type) ;
– masses molaires atomiques M(g·mol-1) :
| H | C | N | O |
| 1,00 | 12,0 | 14,0 | 16,0 |
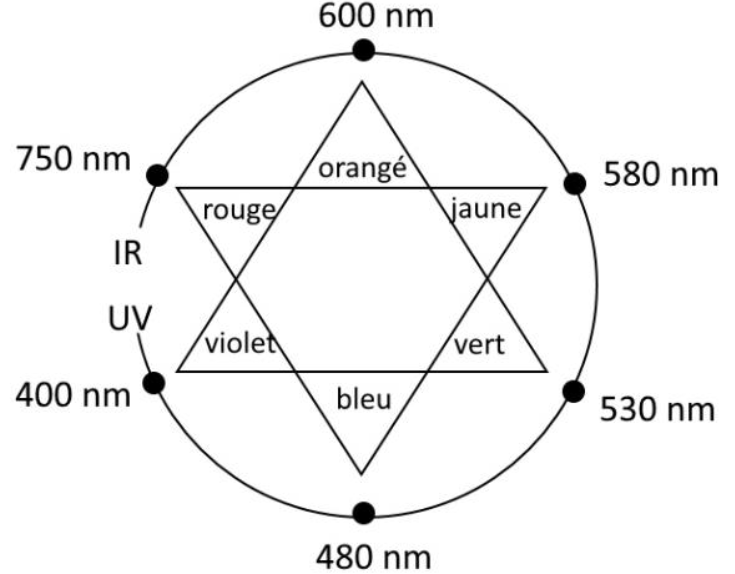
– cercle chromatique :
A. La synthèse de l’urée par Wöhler
Ayant maitrisé la synthèse de l’acide cyanique, Friedrich Wöhler cherchait à préparer du cyanate d’ammonium par réaction du cyanate de potassium (K+(aq) + CNO–(aq)) sur le chlorure d’ammonium (NH4+(aq) + Cℓ–(aq)). Mais le cyanate d’ammonium (NH4+(aq) + CNO–(aq)) obtenu s’isomérise spontanément en cristaux d’urée CH4N2O. L’ensemble du processus est schématisé ci-dessous.
$$ \mathrm{N\equiv C-O^-K^+(aq)}+\mathrm{Cl^-NH_4^+(aq)}\rightarrow\mathrm{N\equiv C-O^-NH_4^+(aq)}\rightarrow\mathrm{CH_4N_2O(aq)} $$
cyanate de potassium + chlorure d’ammonium → cyanate d’ammonium + urée
Q.1. Montrer que le cyanate d’ammonium et l’urée sont bien des isomères.
| Formule brute | |
| Cyanate d’ammonium (NH4 +(aq) + CNO–(aq)) | CH4N2O |
| Urée, une molécule de formule brute CH4N2O | CH4N2O |
Le cyanate d’ammonium et l’urée ont des formules brutes identiques et des formules développées différentes : ce sont des isomères.
Q.2. Choisir parmi les trois propositions suivantes la formule semi-développée de l’urée. Justifier.

| Formule brute | ||
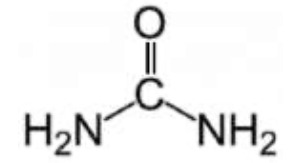 | CH4N2O | Urée |
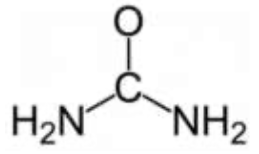 | CH4N2O | Le carbone fait 4 liaisons et l’oxygène en fait 2 : la formule n’est pas bonne. |
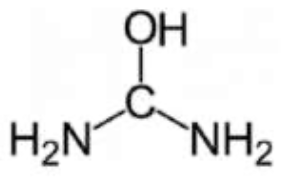 | CH5N2O | La formule brute n’est pas celle de l’urée. |
Q.3. Montrer que le spectre infrarouge obtenu pour les cristaux d’urée est cohérent avec la formule semi-développée proposée.
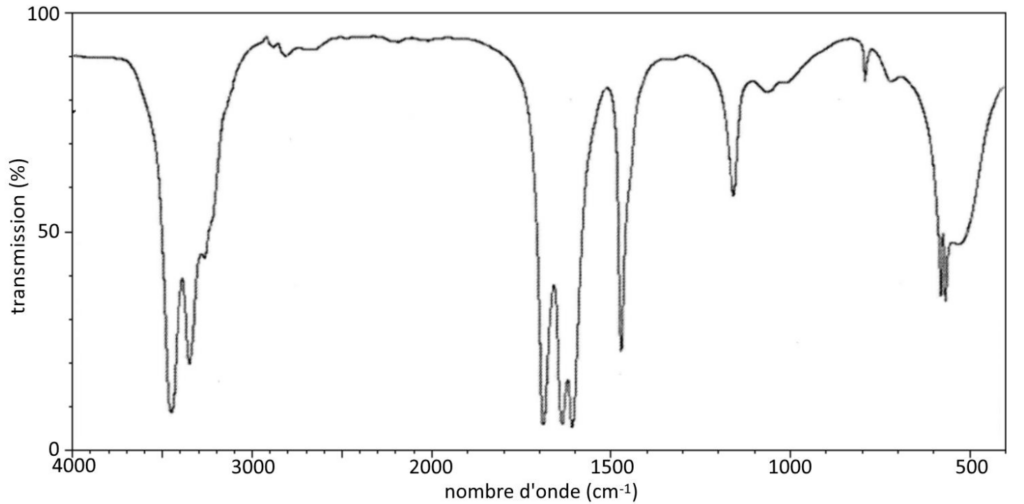
Figure 1. Spectre infrarouge de l’urée (KBr-médiachimie)
Le spectre infrarouge obtenu pour les cristaux d’urée comporte :
- Une bande d’absorption entre 1650 – 1740 correspondant à une liaison C = O d’un amide
- Une bande d’absorption entre 3100 – 3500 correspondant à une liaison N-H d’un amide
- Une bande d’absorption entre 1560 – 1640 correspondant à une liaison N-H d’un amide
Le spectre infrarouge obtenu pour les cristaux d’urée est cohérent avec la formule semi-développée proposée.
B. Dosages de l’urée
Soit une solution aqueuse S d’urée de concentration en quantité de matière C = 6,7 mmol·L-1.
Q.4. Déterminer la masse de cristaux d’urée à peser pour préparer 50,0 mL d’une solution S d’urée de concentration en quantité de matière C = 6,7 mmol·L-1.
Masse de cristaux d’urée à peser :
$$n=\frac{m}{M}$$
$$m=n\times M$$
Or
$$n=C\times V$$
D’ou
$$m=C\times V\times M$$
$$m=6,7\times {10}^{-3}\times 50\times {10}^{-3}\times 60,06$$
$$m=2,0\times {10}^{-2}\ g$$
Dosage gravimétrique
La première technique de dosage de l’urée a été proposée en 1928 par Richard Fosse qui observa la formation de cristaux incolores en mélangeant une solution d’urée et une solution de xanthydrol. Richard Fosse publia alors le protocole précis de cette transformation qui consiste à ajouter à une solution d’urée une solution de xanthydrol puis à filtrer les cristaux incolores de dixanthylurée formés sur un papier filtre. La dixanthylurée est très insoluble dans l’eau à la différence de l’urée. Les cristaux, après séchage, se détachent et sont pesés.
| Xanthydrol | Dixanthylurée |
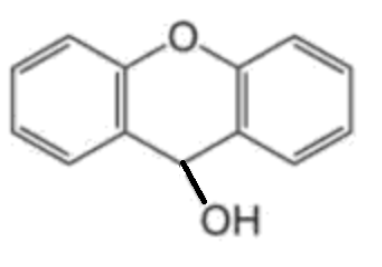 | 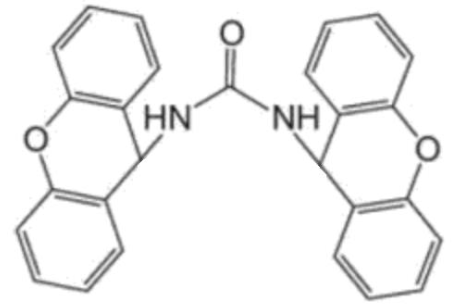 |
| C13H10O2 | C27H20N2O3 |
Figure 2. Formules topologiques et brutes des molécules de xanthydrol et dixanthylurée
L’équation de réaction support du dosage gravimétrique de l’urée est :
2 C13H10O2(aq) + CH4N2O(aq) → C27H20N2O3(aq) + 2 A
Q.5. Identifier l’espèce chimique moléculaire A. Justifier.
2 C13H10O2(aq) + CH4N2O(aq) → C27H20N2O3(aq) + 2 A
| Réactifs | Produits | Manque | |
| Carbone | $2\times 13+1=27$ | 27 | $27-27=0$ |
| Hydrogène | $2\times 10+4=24$ | 20 | $24-20=4$ |
| Oxygène | $2\times 2+1=5$ | 3 | $5-3=2$ |
| Azote | 2 | 2 | $2-2=0$ |
Il manque 4 atomes d’hydrogène et 2 atomes d’oxygène pour 2 molécule A soit 2 atomes d’hydrogène et 1 atome d’oxygène pour une molécule A . A est de Formule H2O.
Q.6. Comparer les masses molaires moléculaires du dixanthylurée et de l’urée et en déduire que la masse de dixanthylurée formée est sept fois supérieure à celle de l’urée consommée.
Dixanthylurée C27H20N2O3
$$M_{Dixanthyluree}=27\times M_C+20\times M_H+2\times M_N+3\times M_O$$
$$M_{Dixanthyluree}=27\times 12,0+20\times 1,00+2\times 14,0+3\times 16,0$$
$$M_{Dixanthyluree}=420\ g{.mol}^{-1}$$
Comparons les masses molaires moleculaires du dixanthyluree et de l’uree :
$$\frac{M_{Dixanthyluree}}{M_{uree}}=\frac{420}{60,06}=6,99$$
La masse molaire du dixanthyluree est sept fois superieure à celle de l’uree.
D’après l’equation de reaction support du dosage gravimetrique :
$$2\ C13H10O2(aq)\ +\ CH4N2O(aq)\ \rightarrow\ C27H20N2O3(aq)\ +\ 2\ A$$
Pour une mole d’uree consommee, une mole de dixanthyluree est produite.
Or la masse molaire du dixanthyluree est sept fois superieure à celle de l’uree.
Ainsi, la masse de dixanthyluree formee est sept fois superieure à celle de l’uree consommee.
$$n_{uree}^{consommee}=n_{dixanthyluree}^{produite}$$
Or $$n=\frac{m}{M}$$
$$\frac{m_{uree}^{consommee}}{M_{uree}}=\frac{m_{dixanthyluree}^{produite}}{M_{Dixanthyluree}}$$
Or
$$M_{Dixanthyluree}=7M_{uree}$$
$$\frac{m_{uree}^{consommee}}{M_{uree}}=\frac{m_{dixanthyluree}^{produite}}{7M_{uree}}$$
$$m_{uree}^{consommee}=\frac{m_{dixanthyluree}^{produite}}{7}$$
$$m_{dixanthyluree}^{produite}=7\times m_{uree}^{consommee}$$
La masse de dixanthyluree formee est sept fois superieure à celle de l’uree consommee.
Afin de vérifier si la solution S a été correctement préparée, un volume V = 1,0 mL ± 0,1 mL de solution S est dosé selon le protocole proposé par Richard Fosse. Le xanthydrol ayant été introduit en excès, une masse de cristaux de dixanthylurée m = 2,7 ± 0,2 mg est mesurée (avec ce qui suit ± correspondant à l’incertitude-type).
Q.7. Montrer que l’expression permettant de calculer la concentration en quantité de matière en urée C de la solution S est :
$$C=\frac{m}{7\cdot M(\text{urée})\cdot V}$$
$$C=\frac{n_{uree}}{V}$$
Or $$n_{uree}=\frac{m_{uree}}{M_{uree}}$$
$$C=\frac{\frac{m_{uree}}{M_{uree}}}{V}=\frac{m_{uree}}{M_{uree}}\times \frac{1}{V}=\frac{m_{uree}}{M_{uree}\times V}$$
Or
$$m_{dixanthyluree}^{produite}=7\times m_{uree}^{consommee}$$
$$m_{uree}^{consommee}=\frac{m_{dixanthyluree}^{produite}}{7}$$
$$C=\frac{\frac{m_{dixanthyluree}^{produite}}{7}}{M_{uree}\times V}=\frac{m_{dixanthyluree}^{produite}}{7}\times \frac{1}{M_{uree}\times V}=\frac{m_{dixanthyluree}^{produite}}{7\times M_{uree}\times V}$$
L’incertitude-type u(C) sur la valeur de la concentration en quantité de matière en urée C obtenue dans la solution S satisfait à la relation :
$$u(C)=C\cdot\sqrt{\left(\frac{u(m)}{m}\right)^2+\left(\frac{u(M(\text{urée}))}{M(\text{urée})}\right)^2+\left(\frac{u(V)}{V}\right)^2}$$
Q.8. Écrire avec un nombre adapté de chiffres significatifs, le résultat de la mesure de C.
$$C=\frac{m_{dixanthyluree}^{produite}}{7\times M_{uree}\times V}$$
$$C=\frac{2,7{\times 10}^{-3}}{7\times 60,06\times 1,0{\times 10}^{-3}}$$
$$C=6,4{\times 10}^{-3}\ mol{.L}^{-1}$$
$$u\left(C\right)=C\cdot \sqrt{\left(\frac{u\left(m\right)}{m}\right)^2+\left(\frac{u\left(M_{uree}\right)}{M_{uree}}\right)^2+\left(\frac{u\left(V\right)}{V}\right)^2}$$
$$u\left(C\right)=6,4{\times 10}^{-3}\ \cdot \sqrt{\left(\frac{0,2}{2,7}\right)^2+\left(\frac{0,01}{60,06}\right)^2+\left(\frac{0,1}{1,0}\right)^2}$$
$$u\left(C\right)=8{\times 10}^{-4}mol{.L}^{-1}$$
$$C=6,4{\times 10}^{-3}\ \pm 8{\times 10}^{-4}mol{.L}^{-1}$$
$$C=\left(6,4\ \pm 0,8\right){\times 10}^{-3}mol{.L}^{-1}$$
Q.9. Vérifier en exploitant le quotient $\frac{\left|C_{\text{mes}}-C_{\text{réf}}\right|}{u(C)}$ que le protocole de Richard Fosse permet de valider que la solution S a été correctement préparée.
$$\frac{\left|C_{mes}-C_{ref}\right|}{u\left(C\right)}=\frac{\left|6,4{\times10}^{-3}\ -6,7{\times10}^{-3}\right|}{8{\times10}^{-4}}=0,4<2$$
Le z-score est inferieur à 2, les résultats sont compatibles.
Le protocole de Richard Fosse permet donc de valider que la solution S a été correctement préparée.
Dosage colorimétrique
Un médecin prescrit une prise de sang à un patient âgé de 20 ans pour diagnostiquer une éventuelle insuffisance rénale. L’urémie est le terme médical utilisé pour qualifier la concentration d’urée contenue dans le sang.
Des techniciens d’un laboratoire d’analyse médicale reçoivent un échantillon sanguin du patient. Ils disposent d’un kit de dosage par étalonnage de l’urée qui s’appuie sur la formation d’une espèce chimique bleue. L’absorbance, notée A, de la solution bleue est directement proportionnelle à la concentration en urée dans l’échantillon, notée C. Elle est mesurée à l’aide d’un spectrophotomètre calibré à une longueur d’onde de 600 nm.
Les résultats du dosage sont :
| ARéférence | CRéférence |
| 1,58 | 6,7 mmol·L-1 |
| AÉchantillon |
| 1,25 |
| Dans le sérum ou le plasma | Intervalle de concentration en urée pour un patient en bonne santé (mmol/L) |
| < 1 an | [1,4-6,8] |
| Enfant | [1,8-6,4] |
| 18-60 ans | [2,1-7,1] |
| 60-90 ans | [2,9-8,2] |
| > 90 ans | [3,6-11,1] |
Q.10. Justifier le choix de la valeur de la longueur d’onde.
Le dosage par étalonnage de l’urée qui s’appuie sur la formation d’une espèce chimique bleue.
La couleur absorbée est la couleur complémentaire au bleu.
Sur le cercle chromatique, la couleur complémentaire au bleu (couleur diamétralement opposée) est l’orangé de longueur d’onde 600nm.
D’ou le choix d’une longueur d’onde de 600nm.

La notice du kit de dosage indique la formule de calcul suivante :
$$C_{\text{échantillon}}=\frac{A_{\text{échantillon}}}{A_{\text{référence}}}\times C_{\text{référence}}$$
Q.11. Démontrer l’égalité indiquée sur la notice de dosage.
D’après la loi de Beer Lambert :
$A=kC$
Ainsi :
$A_{Echantillion}=kC_{Echantillion}$
$kC_{Echantillion}=A_{Echantillion}$
$C_{Echantillion}=\frac{A_{Echantillion}}{k}$
Or
$A_{Reference}=kC_{Reference}$
$kC_{Reference}=A_{Reference}$
$k=\frac{A_{Reference}}{C_{Reference}}$
Donc
$C_{Echantillion}=\frac{A_{Echantillion}}{\frac{A_{Reference}}{C_{Reference}}}$
$C_{Echantillion}=A_{Echantillion}\times\frac{C_{Reference}}{A_{Reference}}$
$C_{Echantillion}=\frac{A_{Echantillion}}{A_{Reference}}\times C_{Reference}$
Q.12. Déterminer la conclusion posée par le médecin quant à une éventuelle urémie élevée chez le patient.
$C_{Echantillion}=\frac{A_{Echantillion}}{A_{Reference}}\times C_{Reference}$
$C_{Echantillion}=\frac{1,25}{1,58}\times 6,7$
$C_{Echantillion}=5,3\ mmol.L^{-1}$
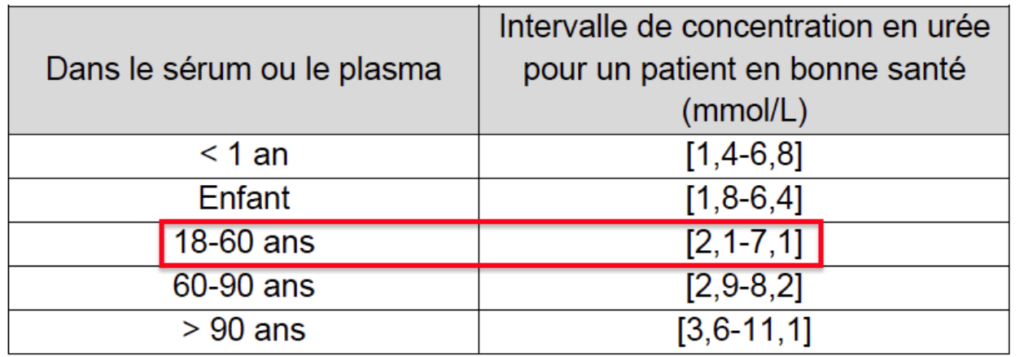
Il s’agit d’une prise de sang à un patient âgé de 20 ans.
D’après le tableau, pour un patient en bonne santé de 20 ans, l’intervalle en urée doit être comprise entre 2,1 et 7,1 mmol/L.
La concentration en urée pour le patient est de 5,3 mmol/L : l’urémie n’est pas élevée, il est en bonne santé.
