Bac Asie 2023 Sujet 1
Exercice 3 – (4,5 points) – Durée 0h47 – Calculatrice autorisée
Sujet n°23-PYCJ1JA1
Sujet et corrigé
EXERCICE III ‒ TENEUR EN ION SALICYLATE DANS UNE CREME (4,5 POINTS)
L’ion salicylate a pour formule chimique C6H4OHCOO‒. Il s’agit d’une espèce chimique que l’on retrouve dans certains médicaments utilisés pour traiter l’acné.
L’étiquette d’un flacon commercial de crème contenant des ions salicylate porte l’indication :
« Ion salicylate formulé à 1000 mg pour 100 g de crème ».
Cela correspond à un pourcentage massique wref = 1 %.
Le but de cet exercice est de contrôler cette indication d’une teneur massique de 1,00 % fournie par le fabricant.
Pour simplifier, on notera HL‒ l’ion salicylate dans tout l’exercice.
Données
- Masse volumique de la crème : ρ(crème) = 860 g·L-1.
- L’ion salicylate en solution aqueuse est obtenu par dissolution du salicylate de sodium solide NaHL dans l’eau ;
- Masse molaire du salicylate de sodium : M(NaHL) = 160,1 g·mol-1.
- Masse molaire de l’ion salicylate : M(HL‒) = 137,1 g·mol-1.
- Concentration standard : c° = 1,0 mol·L-1.
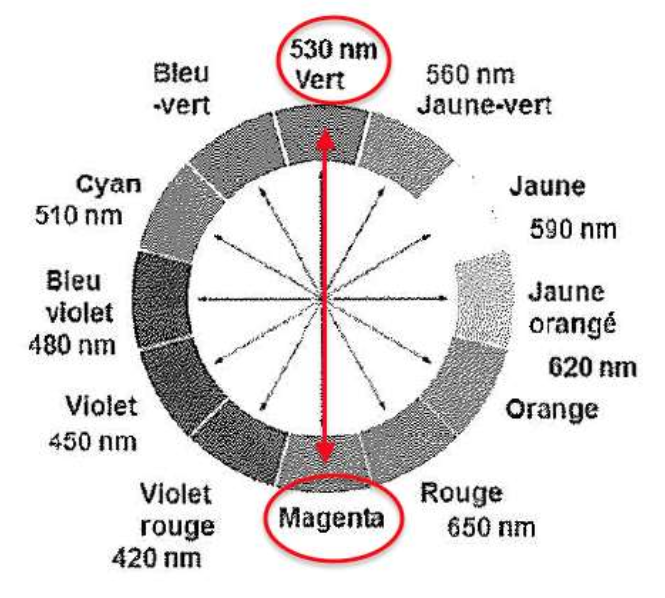
- Cercle chromatique :
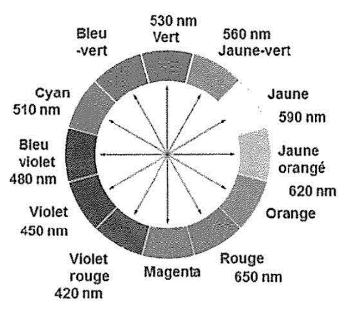
L’ion salicylate absorbe dans le domaine des ultraviolets et ne peut donc pas être détecté par un spectrophotomètre fonctionnant dans le visible. Mais lorsqu’il réagit avec des ions Fe3+, l’ion salicylate HL‒ forme une espèce colorée qu’il est possible de doser à l’aide du spectrophotomètre.
Dans la partie A, on cherche à vérifier que la réaction entre l’ion Fe3+ et l’ion HL‒ en solution aqueuse est totale.
Dans la partie B, on réalise le dosage spectrophotométrique de l’espèce colorée continue.
Partie A – Étude de la réaction entre l’ion Fe3+ et l’ion HL‒
L’équation de cette réaction est :
Fe3+(aq) + HL‒(aq) ⇌ FeL+(aq) + H+(aq) (équation 1)
Peu colorée incolore très colorée incolore
On note K = 102,9 la constante d’’équilibre de cette réaction à la température de 25°C.
On prépare une solution aqueuse Sfer contenant des ions Fe3+ en solution aqueuse de concentration Cfer = 10,0 mmol·L‒1 = [Fe3+]. Cette solution est de plus une solution tampon dont la valeur du pH est pH = 3,0.
On dispose d’une solution aqueuse « mère » S0 de salicylate de sodium (Na+, HL‒) de concentration C0 = 100 mmol·L‒1.
À partir de la solution S0, on prépare une solution diluée S1 de concentration C1 = 10,0 mmol·L‒1.
1. Déterminer la masse m de salicylate de sodium NaHL solide qu’il a fallu peser pour préparer un volume V0 = 100,0 mLde la solution aqueuse S0 de concentration C0.
$$n=\frac{m}{M}$$
$$m=n\times M$$
Or $$n=C_0\times V_0$$
D’ou :
$$m=C_0\times V_0\times M$$
$$m=100{\times 10}^{-3}\times 100,0{\times 10}^{-3}\times 160,1$$
$$m=1,60\ g$$
Il a fallu peser 1,60g de salicylate de sodium pour préparer 100,0mL de la solution S0.
2. Identifier dans la liste ci-dessous la verrerie à utiliser pour préparer V1 = 50,0 mL de la solution S1 à partir de la solution mère S0. Justifier à l’aide d’un calcul.
Verrerie à disposition :
- fioles jaugées de 10,0 mL et 50,0 mL
- pipettes jaugées de 2,0 mL ; 5,0 mL ; 10,0 mL et 20,0 mL
Lors d’une dilution, la quantité de matière se conserve :
$$n_0=n_1$$
$$C_0V_0=C_1V_1$$
$$V_0=\frac{C_1V_1}{C_0}$$
$$V_0=\frac{10,0{\times 10}^{-3}\times 50,0{\times 10}^{-3}}{100,0{\times 10}^{-3}}$$
$$V_0=5,00\ {\times 10}^{-3}L$$
$$V_0=5,00\ mL$$
On choisit :
une fiole jaugée V1=50,0 mL
une pipette jaugée V0=5,00 mL
Le milieu réactionnel est obtenu en mélangeant dans un bécher :
- un volume Vfer = 10,0 mL de la solution Sfer tamponnée de concentration Cfer ;
- un volume V = 0,100 mL de la solution diluée S1 de concentration C1 ;
3. Après avoir rappelé les propriétés d’une solution tampon, justifier que la valeur du pH du milieu réactionnel ne varie pas.
Une solution tampon est une solution qui maintient approximativement le même pH malgré l’addition de petites quantités d’un acide ou d’une base, ou malgré une dilution.
On ajoute à une solution tamponnée de 10,0 mL un volume 0,100 mL de solution S1 : le volume ajouté est petit devant le volume de la solution tamponnée. La valeur du pH de la solution du milieu réactionnel ne varie donc pas.
4. Compléter littéralement le tableau d’avancement de la réaction en annexe à rendre avec la copie. On note xéq l’avancement à l’état d’équilibre, exprimé en mol.
| Équation | Fe3+(aq) + HL‒(aq) ⇌ FeL+(aq) + H+(aq) | |||
| État initial | Cfer x Vfer | C1 x V | 0 | n(H+) constante |
| État d’équilibre | $$C_{fer}\times V_{fer}-x_{eq}$$ | $$C_1\times V-x_{eq}$$ | $$x_{eq}$$ | |
5. Montrer qu’à l’équilibre du système chimique, la constante d’équilibre K de cette réaction peut se mettre sous la forme : $K=\frac{x_{\mathrm{eq}}\times[H^+]\times\left(V+V_{\mathrm{fer}}\right)}{\left(C_{\mathrm{fer}}\times V_{\mathrm{fer}}-x_{\mathrm{eq}}\right)\times\left(C_1\times V-x_{\mathrm{eq}}\right)} $
$$K=Q_{r,eq}=[FeL+]{eq}\times H^+{eq}[Fe^{3+}]{eq}\times[HL^-]{eq}$$
Or
$$[Fe^{3+}]{eq}=\frac{C{fer}\times V_{fer}-x_{eq}}{V+V_{fer}}$$
$$\left[{\rm HL}^-\right]{eq}=\frac{C_1\times V-x{eq}}{\left(V+V_{fer}\right)}$$
$$\left[{\rm FeL}^+\right]{eq}=\frac{x{eq}}{\left(V+V_{fer}\right)}$$
D’ou
$$K=\frac{\frac{x_{eq}}{\left(V+V_{fer}\right)}{\times\left[H^+\right]}{eq}}{\frac{C{fer}\times V_{fer}-x_{eq}}{\left(V+V_{fer}\right)}\times \frac{C_1\times V-x_{eq}}{\left(V+V_{fer}\right)}}$$
$$K=\frac{x_{eq}}{\left(V+V_{fer}\right)}{\times\left[H^+\right]}{eq}\frac{V\times V}{\left(C{fer}\times V_{fer}-x_{eq}\right)\times \left(C_1\times V-x_{eq}\right)}$$
$$K=\frac{x_{eq}}{\left(V+V_{fer}\right)}{\times\left[H^+\right]}{eq}\frac{\left(V+V{fer}\right)\times \left(V+V_{fer}\right)}{\left(C_{fer}\times V_{fer}-x_{eq}\right)\times \left(C_1\times V-x_{eq}\right)}$$
$$K=\frac{{x_{eq}\times \left[H^+\right]}{eq}\left(V+V{fer}\right)}{\left(C_{fer}\times V_{fer}-x_{eq}\right)\times \left(C_1\times V-x_{eq}\right)}$$
L’application numérique conduit à l’égalité suivante (qui n’est pas à démontrer) :
$$ K=\frac{x_{\mathrm{eq}}\times[H^+]\times\left(V+V_{\mathrm{fer}}\right)}{\left(C_{\mathrm{fer}}\times V_{\mathrm{fer}}-x_{\mathrm{eq}}\right)\times\left(C_1\times V-x_{\mathrm{eq}}\right)}. $$
Mathématiquement, cette équation en xéq admet deux solutions que l’on peut écrire :
x1 = 9,999´10‒7 mol et x2 = 9,999´10‒5 mol.
6. Indiquer pourquoi il convient de ne retenir que la valeur x1 et déduire de cette valeur que la réaction peut être considérée comme totale.
Calculons $$x_{max}$$ :
$$C_{fer}\times V_{fer}-x_{max1}=0$$
$$x_{max1}=C_{fer}\times V_{fer}$$
$$x_{max1}=10,0{\times 10}^{-3}\times 10,0{\times 10}^{-3}$$
$$x_{max1}=1,0{\times 10}^{-4}\ mol$$
$$C_1\times V-x_{max2}=0$$
$$x_{max2}=C_1\times V$$
$$x_{max2}=10,0{\times 10}^{-3}\times 0,100{\times 10}^{-3}$$
$$x_{max2}=1,0{\times 10}^{-6}\ mol$$
$$x_{max2}<x_{max1}$$
$$x_{max}=x_{max2}=1,0{\times 10}^{-6}\ mol$$
Or $$x_{eq}\le x_{max}$$, parmi les deux solutions, nous ne pouvons prendre $$x_2$$ car $$x_2>x_{max}$$.
On ne peut donc garder que la valeur $$x_1$$.
$$\tau=\frac{x_{eq}}{x_{max}}$$
$$\tau=\frac{x_1}{x_{max}}$$
$$\tau=\frac{9,999{\times 10}^{-7}}{1,0{\times 10}^{-6}}$$
$$\tau=0,9999$$
$$\tau=1,0$$ (Règle des arrondis)
La réaction peut être considéré comme totale.
Partie B – Dosage spectrophotométrique des ions salicylate HL‒
La partie A a permis de conclure que la réaction entre l’ion Fe3+ et l’ion HL‒ peut être considérée comme totale. Pour la réaction d’équation 1, on a donc l’égalité :
n(FeL+)(produit) = n(HL–)(réagi)
L’espèce produite FeL+ est dosée par spectrophotométrie et étalonnage.
Le spectre d’absorption de l’espèce FeL+ est présenté sur la figure 1 ci-dessous.
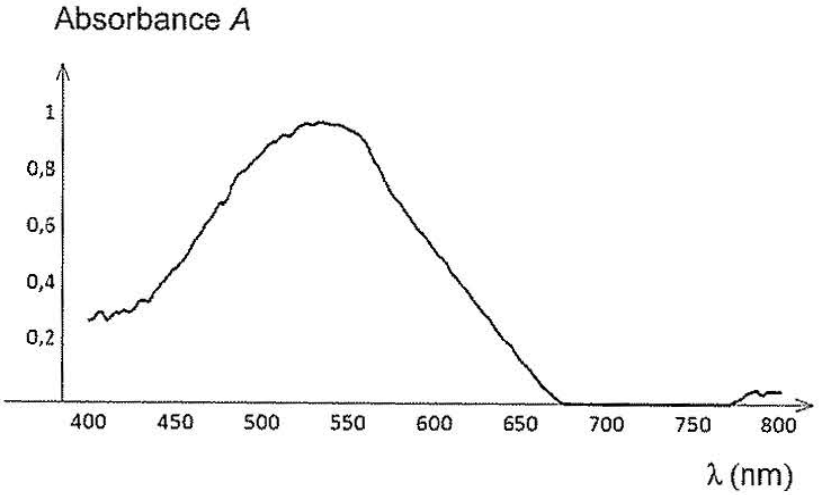
Figure 1 ‒ Spectre d’absorption de l’espèce FeL+
Pour tracer la courbe d’étalonnage, on a préparé cinq solutions étalons en mélangeant :
- un volume Vfer = 10,0 mL de solution Sfer ;
- un volume V = 0,100 mL d’une solution de salicylate de sodium de concentration Ci connue ;
Pour λmax = 535 nm, on a mesuré l’absorbance de chaque solution étalon, ce qui a permis de tracer le graphique en figure 2 présentant l’évolution de l’absorbance en fonction de la concentration en ion HL‒.
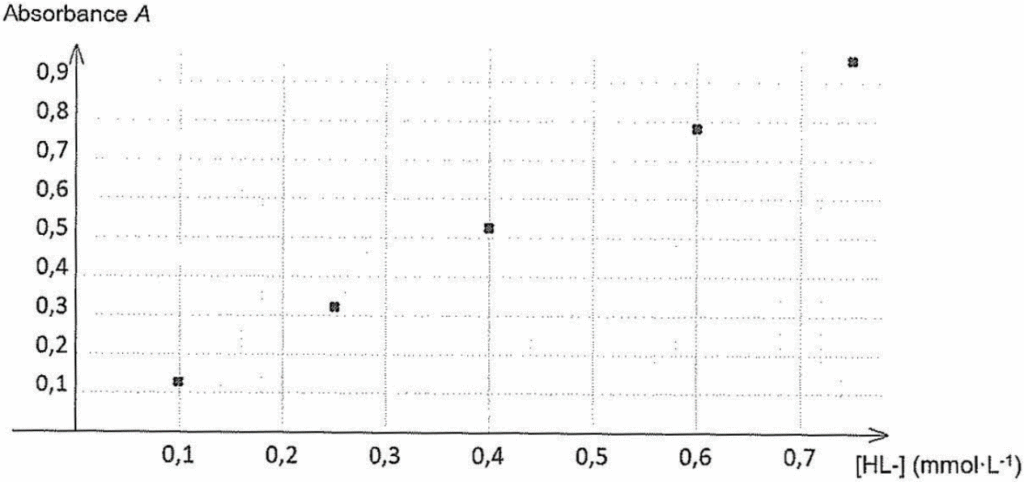
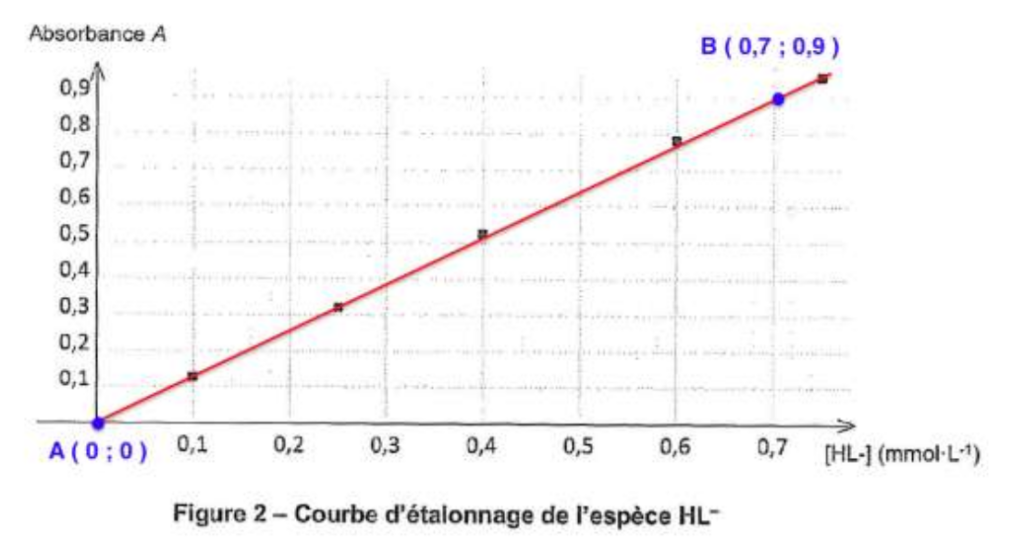
Figure 2 ‒ Courbe d’étalonnage de l’espèce HL‒
Pour déterminer la teneur en ion salicylate HL‒ dans la crème étudiée, on mesure l’absorbance d’une solution test préparée de la même manière que les solutions étalons, soit en mélangeant :
- un volume Vcrème = 0,100 mL de la crème étudiée contre l’acné ;
- un volume Vfer = 10,0 mL de solution Sfer.
L’absorbance mesurée à l = 535 nm de cet échantillon a pour valeur : Acrème = 0,83.
7. Indiquer la couleur de l’espèce chimique FeL+ à partir de son spectre d’absorption (figure 1).
On choisit la longueur d’onde correspondante au maximum de l’absorbance :
$$\lambda_m=535\ nm$$
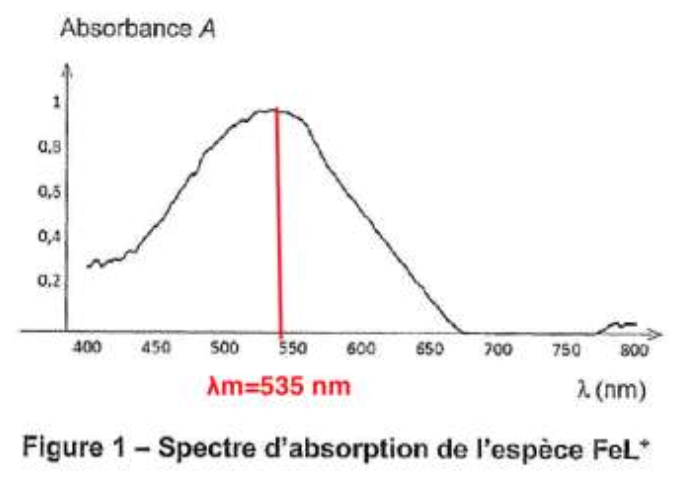
$$\lambda_m=535\ nm$$ : la couleur absorbée est le vert
La couleur de l’espèce ${\rm FeL}^+$ est la couleur complémentaire. La couleur complémentaire est celle opposée sur le cercle chromatique.
La couleur de l’espèce ${\rm FeL}^+$ est magenta.
8. À partir de la figure 2, déterminer la quantité de matière en ion salicylate HL‒ présente dans la crème et en déduire le pourcentage massique mesuré wmes en ions salicylate dans la crème contre l’acné.
Méthode 1 :
Graphiquement, A=f(c) est une droite passant par l’origine. La loi de Beer Lambert est vérifiée.
Trouvons le coefficient directeur K
$$k=\frac{y_B-y_A}{x_B-x_A}$$
$$k=\frac{0,90-0}{0,70-0}$$
$$k=1,29\ L.{\rm mmol}^{-1}$$
$$A=1,29\ C$$
$$A_{crème}=0,83$$ $$A=1,29\ C$$
$$1,29\ C=A$$
$$C=\frac{A}{1,29}$$
$$C=\frac{0,83}{1,29}$$
$$C=0,64\ \ mmol.L^{-1}$$
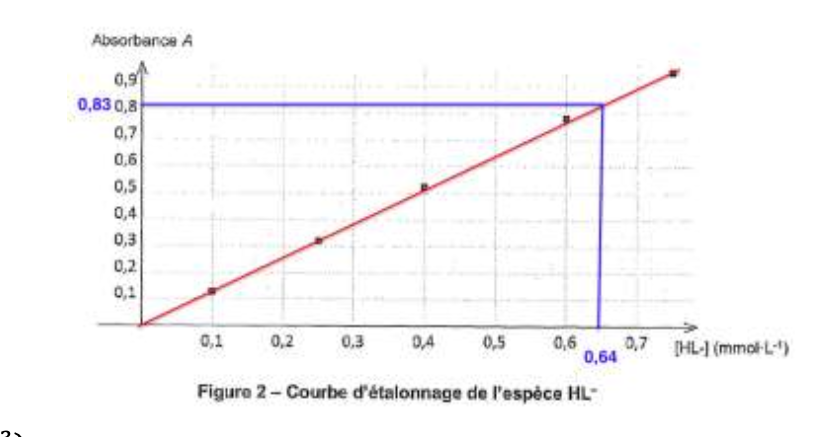
Méthode 2 :
Graphiquement pour $A_{crème}=0,83$,
$C=0,64\ \ mmol.L^{-1}$
$$n=C\times V$$
$$n=C\times V_{crème}+V_{fer}$$
$$n=0,64{\times 10}^{-3}\times \left(0,100{\times 10}^{-3}+10,0{\times 10}^{-3}\right)$$
$$n=6,5{\times 10}^{-6}\ mol$$
$$w_{mes}=\frac{m}{m_{crème}}$$
$$m=n\times M$$
$$m_{crème}=\rho_{crème}\times V_{crème}$$
$$w_{mes}=\frac{n\times M}{\rho_{crème}\times V_{crème}}$$
$$w_{mes}=\frac{6,5{\times 10}^{-6}\times 137,1}{860\times 0,100{\times 10}^{-3}}$$
$$w_{mes}=0,0103$$
$$w_{mes}=1,03%$$
Le pourcentage massique en ion salicylate mesuré dans la crème est 1,03%.
Il est possible de comparer une valeur expérimentale (wmes) à la valeur de référence (wref) en utilisant le quotient $\frac{\left|w_{\mathrm{mes}}-w_{\mathrm{ref}}\right|}{u(w)}$, où u(w) est l’incertitude-type sur le résultat expérimental.
Dans le cas présent, on considère que la valeur mesurée wmes est compatible avec la valeur wref si le quotient est inférieur ou égal à 2.
On admet que, pour ce dosage, u(w) = 0,02 %.
9. Comparer le résultat obtenu expérimentalement à celui indiqué sur l’étiquette du flacon.
$$z\ =\frac{\left|w_{mes}\ -\ w_{ref}\right|}{u\left(w\right)}$$
$$z\ =\frac{\left|1,03\ -\ 1,00\right|}{0,02}$$
$$z\ =1,5$$
Le z-score est inférieur à 2 : le pourcentage obtenu expérimentalement est compatible à la valeur indiquée sur l’étiquette du flacon.
Exercice III
Question 4
Tableau d’avancement en quantité de matière du milieu réactionnel (réaction d’équation 1).
On note xéq l’avancement à l’état d’équilibre, en mol.
| Équation | Fe3+(aq) + HL‒(aq) ⇌ FeL+(aq) + H+(aq) | |||
| État initial | Cfer x Vfer | C1 x V | 0 | n(H+) constante |
| État d’équilibre | ||||
