Un emballage intelligent au rayon poissonnerie

Métropole 2025 Sujet 1

Exercice 1 – (9 points) –  Durée 1h35 – Calculatrice autorisée

Sujet n°25-PYCJ1ME1

Dans cet exercice, on souhaite vérifier si le bleu de bromophénol, un indicateur coloré acide-base noté BBP dans la suite de l’exercice, peut convenir pour la réalisation de ce type de pastille.

1.  Synthèse du bleu de bromophénol

Pour synthétiser et caractériser le BBP (C₁₉H₁₀Br₄O₅S), on réalise le protocole suivant : 
– étape n°1 : dissoudre dans un erlenmeyer une masse m = 201 mg de rouge de phénol (C₁₉H₁₄O₅S) dans 10 mL d’éthanol. Agiter, puis ajouter goutte à goutte une solution contenant du perbromure de pyridinium, qui permet de libérer du dibrome Br₂ dans le milieu ;
– étape n°2 : éliminer le solvant jusqu’à obtenir des cristaux au fond du ballon. Filtrer puis sécher les cristaux à l’étuve. Le produit solide obtenu est appelé par la suite le produit synthétisé brut ;
– étape n°3 : réaliser une chromatographie sur couche mince des réactifs et du produit synthétisé brut ;
– étape n°4 : enregistrer les spectres d’absorption du BBP de référence et du produit synthétisé brut.

Données :

• équation de la réaction modélisant la synthèse du BBP :

$$\mathrm{C_{19}H_{14}O_5S_{(solv)} + 4\ Br_{2(solv)} \rightarrow C_{19}H_{10}Br_4O_5S_{(solv)} + 4\ HBr_{(solv)}}$$

où (solv) signifie dissous dans le solvant, ici l’éthanol ;

• concentration standard : c° = 1 mol·L^–1 ;
• température de fusion du BBP : θ _fusion = 273 °C ;
• pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on peut utiliser le quotient $\left|\dfrac{x-x_{\mathrm{ref}}}{u(x)}\right|$ avec $x$ la valeur mesurée, $x_{\mathrm{ref}}$ la valeur de référence et $u(x)$ l’incertitude-type associée à la valeur mesurée $x$ ;
• chromatogramme obtenu du produit synthétisé brut (les espèces étant dissoutes dans un solvant adapté) :

• spectres d’absorption du BBP de référence et du produit synthétisé brut :

Q1. Donner un titre aux étapes du protocole, en choisissant parmi les propositions suivantes : analyse du produit brut ; transformation des réactifs ; séparation.

Titre aux étapes du protocole :

– étape n°1 : transformation des réactifs

– étape n°2 : séparation

– étape n°3 : analyse du produit brut

– étape n°4 : analyse du produit brut

Q2. En vous appuyant sur le chromatogramme obtenu, montrer qu’une transformation chimique a eu lieu et préciser si le produit synthétisé brut est pur.

Les réactifs de la synthèse sont :

Le rouge de phénol

Le perbromure de pyridinium, qui permet de libérer du dibrome Br2 dans le milieu ;

L’analyse du produit synthétisé brut à l’état final montre :

Une tâche qui est au même niveau que le produit b (perbromure de pyridinium).

Une tâche qui n’est pas au même niveau que le produit a (rouge de phénol).

Ainsi, le produit final est un mélange (2 taches verticales) qui contient un des réactifs et une espèce différente de l’autre réactif : une transformation chimique a eu lieu et le produit synthétisé brut n’est pas pur.

Q3. À l’aide des spectres d’absorption proposés, justifier que le produit brut contient du BBP.

Les spectres d’absorption proposés du BBP de référence et du produit synthétisé brut ont un même λ_max et une forme similaire.

Ainsi, le produit brut contient du BBP.

Remarque : La différence observée entre 400 nm et 500 nm vient certainement du fait que le produit n’est pas pur.

Q4. Citer une autre méthode permettant d’identifier le produit brut.

Autre méthode permettant d’identifier le produit brut : Spectroscopie IR

2.  Identification du produit synthétisé par une mesure de pKA

Le produit brut obtenu est purifié. On se propose d’en déterminer la constante d’acidité associée pour confirmer qu’il s’agit de BBP, en étudiant la courbe de titrage d’une solution contenant cette espèce par une solution aqueuse d’hydroxyde de sodium.

Q5. Le BBP est un indicateur coloré acide-base dont le couple acide-base est noté BH₂(aq) / BH^–(aq). Donner l’expression de la constante d’acidité KA de ce couple en fonction de [BH₂], [BH^–], [H₃O⁺], concentrations des espèces à l’équilibre chimique, ainsi que de la concentration standard c°.

$K_A=\dfrac{\left[{\rm BH}^-\right]{eq}\times\left[H_3O^+\right]{eq}}{\left[BH_2\right]{eq}\times c^0}$

Q6. À partir de l’expression précédente, établir la relation suivante :

$$pH = pK_A + \log\left(\dfrac{[\mathrm{BH^-}]}{[\mathrm{BH_2}]}\right)$$

$K_A=\dfrac{\left[{\rm BH}^-\right]{eq}\times\left[H_3O^+\right]{eq}}{\left[BH_2\right]{eq}\times c^0}$
$-log\left(K_A\right)=-log\left(\dfrac{\left[{\rm BH}^-\right]{eq}\times\left[H_3O^+\right]{eq}}{\left[BH_2\right]{eq}\times c^0}\right)$
$-log\left(K_A\right)=-log\left(\dfrac{\left[{\rm BH}^-\right]{eq}}{\left[BH_2\right]{eq}}\times\dfrac{\left[H_3O^+\right]{eq}}{c^0}\right)$
$-log\left(K_A\right)=-log\left(\dfrac{\left[{\rm BH}^-\right]{eq}}{\left[BH_2\right]{eq}}\right)-log\left(\dfrac{\left[H_3O^+\right]{eq}}{c^0}\right)$
${\rm pK}A=-log\left(\dfrac{\left[{\rm BH}^-\right]{eq}}{\left[BH_2\right]{eq}}\right)+pH$
${\rm pK}A+log\left(\dfrac{\left[{\rm BH}^-\right]{eq}}{\left[BH_2\right]{eq}}\right)=pH$
$pH={\rm pK}A+log\left(\dfrac{\left[{\rm BH}^-\right]{eq}}{\left[BH_2\right]{eq}}\right)$

On prépare une solution Sa du produit de synthèse purifié. On réalise un titrage de la solution Sa à l’aide d’une solution Sb d’hydroxyde de sodium, suivi par pH-métrie.

L’équation de la réaction support du titrage est :

BH₂(aq) + OH^–(aq) → BH^–(aq) + H₂O(ℓ)

La courbe de titrage est donnée sur la figure 1 ci-dessous.

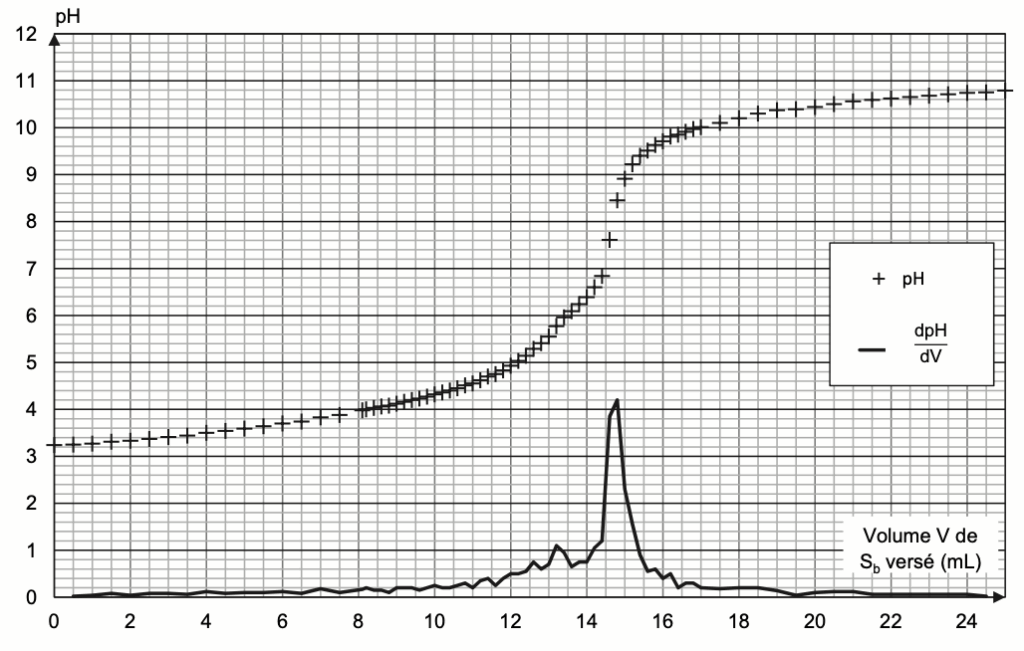
Figure 1. Courbes de suivi pH-métrique et dérivée dV du titrage de la solution Sa

Q7. Définir l’équivalence d’un titrage.

L’équivalence est atteinte lorsque les réactifs sont introduits dans des proportions stœchiométriques.

Q8. En explicitant la méthode, déterminer le volume V_E de solution S_b versé à l’équivalence.

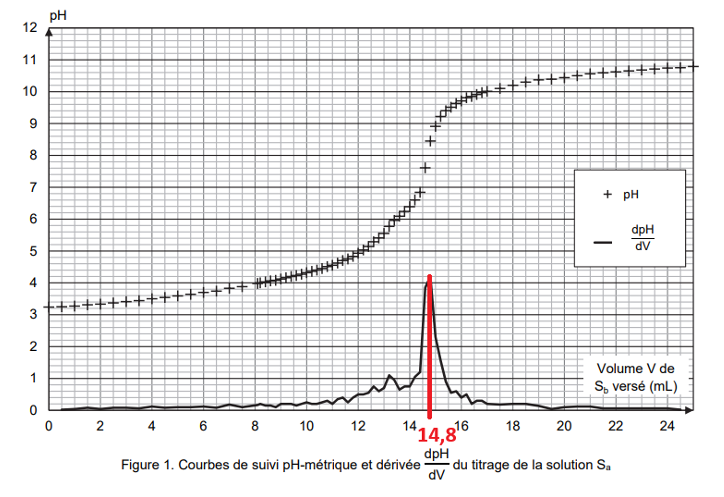
Pour déterminer expérimentalement le $pK_A$ du couple $\mathrm{BH_{2(aq)}/BH^-_{(aq)}}$, on s’intéresse à un point particulier de la courbe, la demi-équivalence, atteint pour un volume versé égal à $\dfrac{V_E}{2}$.

Q9. Montrer que [BH^–]= [BH₂] à la demi-équivalence.

À la demi-équivalence $V=\dfrac{V_E}{2}$
La moitié des molécules de BH₂ ont été consommés.
Ainsi :
$\left[BH_2\right]_{demi\ eq}=\dfrac{\left[BH_2\right]0}{2}$
Or pour chaque BH₂ qui réagit, un ion ${\rm BH}^-$ apparait.
Ainsi :
$\left[{\rm BH}^-\right]{demi\ eq}=\dfrac{\left[BH_2\right]_0}{2}$

D’où, à la demi-équivalence :
$\left[{\rm BH}^-\right]{demi\ eq}=\left[BH_2\right]{demi\ eq}$

Q10. En déduire, en explicitant la démarche utilisée, la valeur expérimentale du pK_A du couple BH₂(aq) / BH^–(aq).

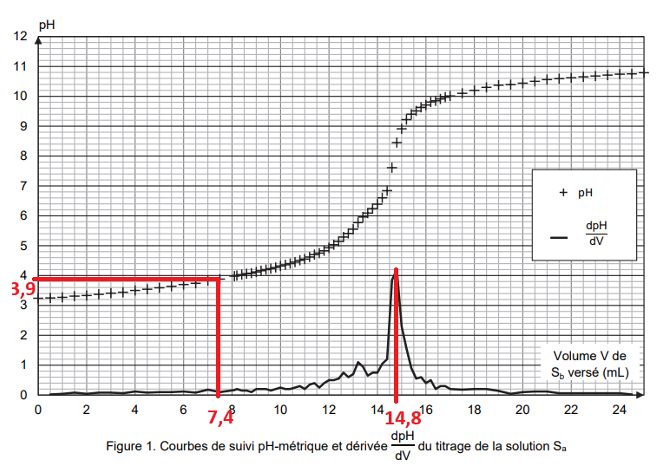
Or, d’après la relation trouvée à la question Q6 :
${\rm pH}{demi\ eq}={\rm pK}A+log\left(\dfrac{\left[{\rm BH}^-\right]{demi\ eq}}{\left[BH_2\right]{demi\ eq}}\right)$
${\rm pH}_{demi\ eq}={\rm pK}A+log\left(1\right)$
${\rm pH}{demi\ eq}={\rm pK}_A$

D’où
${\rm pK}A={\rm pH}{demi\ eq}$
${\rm pK}_A=3,9$

Q11. Sachant que la valeur tabulée du pK_A à 25 °C de ce couple est égale à 4,1, indiquer si la valeur obtenue à la question Q10 est compatible avec la présence de BBP dans le produit de synthèse purifié. L’incertitude- type sur la mesure du pKA est évaluée à u(pKA) = 0,3.

D’après les données : pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on peut utiliser le quotient :
$\dfrac{\left|x-x_{ref}\right|}{u\left(x\right)}$

$\dfrac{\left|{\rm pK}_A-{{\rm pK}A}{ref}\right|}{u\left({\rm pK}_A\right)}=\dfrac{\left|3,9-4,1\right|}{0,3}$
$\dfrac{\left|{\rm pK}_A-{{\rm pK}A}{ref}\right|}{u\left({\rm pK}_A\right)}=0,67$
$\dfrac{\left|{\rm pK}_A-{{\rm pK}A}{ref}\right|}{u\left({\rm pK}_A\right)}<2$
Ainsi, la valeur obtenue à la question Q10 est compatible avec la présence de BBP dans le produit de synthèse purifié.

3.  Étude de la couleur de la pastille dans l’emballage intelligent

Une pastille est imprégnée par une solution de BBP. Cet indicateur coloré a des formes acide et basique de couleurs différentes en solution. On donne ci-dessous le spectre d’absorption d’une solution aqueuse contenant majoritairement la forme acide :

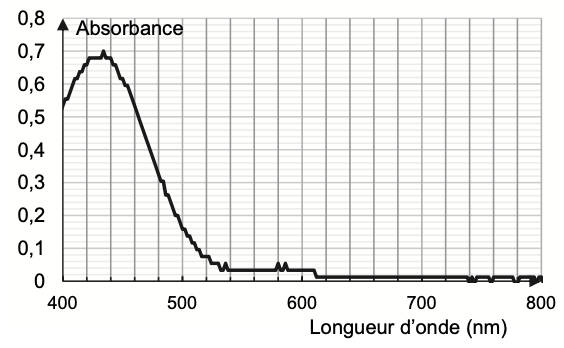
Figure 2. Spectre d’absorption d’une solution aqueuse de BBP de pH = 2,0, contenant majoritairement la forme acide

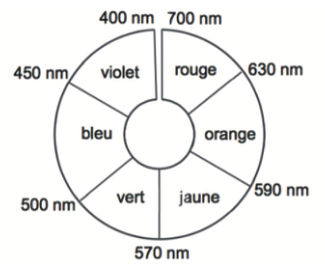
Figure 3. Cercle chromatique

Données :

• une solution contenant majoritairement la forme basique du BBP est de couleur bleue ;
• masse volumique de l’eau à 20 °C : ρ_eau = 1,0 kg·L^–1 ;
• masse molaire du chlorure d’hydrogène : M = 36,5 g·mol^–1 ;
• règles de nomenclature :
  • pour les squelettes carbonés :

Pour les hydrocarbures ramifiés, la position de la ramification sur la chaine principale est indiquée par un chiffre et le groupe est indiqué par le préfixe. Si plusieurs groupes sont identiques, on précède le préfixe par di, tri ou tétra, respectivement pour 2, 3 ou 4 groupes identiques.
Méthyl CH3 –	Éthyl CH3 – CH2 –	Propyl CH3 – CH2 – CH2 –

pour les dérivés de l’ammoniac :

Q12. Montrer que la solution contenant la forme acide du BBP est de couleur jaune.

Pour obtenir le spectre de la figure 2, il est nécessaire de préparer une solution d’acide chlorhydrique de pH = 2,0. La solution commerciale utilisée au laboratoire est de titre massique t_m = 37 % et de densité d = 1,18. On dispose de pipettes jaugées de volumes usuels entre 1,0 mL et 50,0 mL et d’une fiole jaugée de volume V = 200,0 mL.

Q13. Montrer qu’il est impossible de préparer cette solution en ne réalisant qu’une seule dilution avec le matériel proposé.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.

Calculons la concentration de la solution commerciale utilisée :
$c=\dfrac{n_{HCl}}{V_{Solution}}$

Or
$n_{HCl}=\dfrac{m_{HCl}}{M_{HCl}}$
Ainsi :

$c=\dfrac{n_{HCl}}{V_{Solution}}=\dfrac{m_{HCl}}{M_{HCl}\times V_{Solution}}$

Or le titre massique (pourcentage) est défini par :
$t_m=\dfrac{m_{HCl}}{m_{solution}}$

D’où
$m_{HCl}=t_m\times m_{solution}$
Ainsi :
$c=\dfrac{m_{HCl}}{M_{HCl}\times V_{Solution}}=\dfrac{t_m\times m_{solution}}{M_{HCl}\times V_{Solution}}$

Or
$\rho_{solution}=\dfrac{m_{solution}}{V_{Solution}}$

Ainsi :
$c=\dfrac{t_m\times m_{solution}}{M_{HCl}\times V_{Solution}}=\dfrac{t_m\times\rho_{solution}}{M_{HCl}}$

Or
$d=\dfrac{\rho_{solution}}{\rho_{eau}}$
$\dfrac{\rho_{solution}}{\rho_{eau}}=d$
$\rho_{solution}=d\times\rho_{eau}$

Ainsi :
$c=\dfrac{t_m\times\rho_{solution}}{M_{HCl}}=\dfrac{t_m\times d\times\rho_{eau}}{M_{HCl}}$

$c=\dfrac{\dfrac{37}{100}\times1,18\times1,0\times 10^3}{36,5}$
$c=12\ mol.L^{-1}$

Solution d’acide chlorhydrique $\left({H_3O}^+;{\rm Cl}^-\right)$
$\left[{H_3O}^+\right]{com}=c$
$\left[{H_3O}^+\right]{com}=12\ mol.L^{-1}$

Calculons la concentration de la solution commerciale diluée :
$H_3O^+{diluée}=c_0\times 10^{-pH}$
$H_3O^+{diluée}=1,0\times 10^{-2,0}$
$H_3O^+_{diluée}=1,0\times 10^{-2}\ mol.L^{-1}$

Lors d’une dilution, la quantité de matière se conserve :
$n_{com}=n_{diluée}$
$\left [{H_3O}^+\right]{com}\times V{mere}=[H_3O^+{diluée}]\times V{fille}$
$V_{mere}=\dfrac{[H_3O^+{diluée}] \times V{fille}}{[H_3O^+_{com}]}$

Remarque : le volume de la solution fille est celui de la fiole jaugée soit $V_{fille}=200,0\ mL$.

$V_{mere}=\dfrac{1,0\times 10^{-2}\times200\times 10^{-3}}{12}$
$V_{mere}=1,7\times 10^{-4}\ L$
$V_{mere}=0,17\ mL$

Pour préparer cette solution en ne réalisant qu’une seule dilution il faudrait une pipette jaugée de 0,17 mL.
Or le matériel proposé ne comporte que pipettes jaugées de volumes usuels entre 1,0 mL et 50,0 mL.

Ainsi, il est impossible de préparer cette solution en ne réalisant qu’une seule dilution avec le matériel proposé.

Au cours du temps, les bactéries contenues dans le poisson produisent naturellement des molécules de N,N-diméthylméthanamine qui entrent en contact avec la pastille imbibée de BBP.

Q14. Choisir, parmi les trois formules semi-développées suivantes, celle qui correspond à la molécule de N,N-diméthylméthanamine.

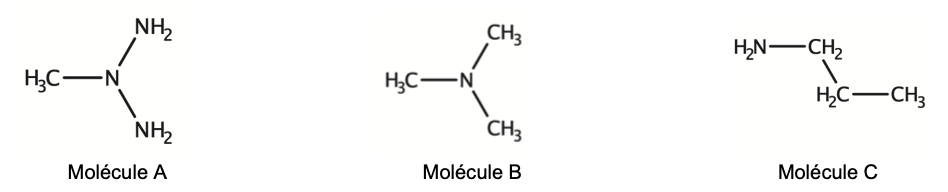
La molécule qui correspond à la molécule de N,N-diméthylméthanamine est la molécule B.

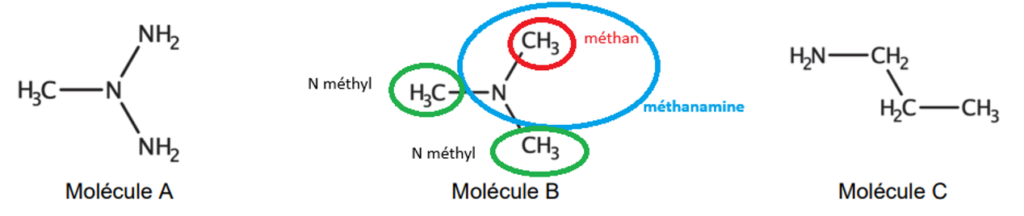
Au cours de la dégradation du poisson, qui se réalise sur plusieurs jours, la N,N-diméthylméthanamine, composé volatil, est produite. La pastille de BBP initialement jaune se colore alors en bleu.

Q15. Écrire l’équation de la réaction modélisant la transformation chimique responsable de ce changement de couleur. On note BH₂(aq) / BH^–(aq) le couple acide-base correspondant au BBP, et R₃NH⁺(aq) / R₃N(aq) celui associé à la N,N-diméthylméthanamine.

On note $BH_{2(aq)}/{{\rm BH}^-}{(aq)}$ le couple acide-base correspondant au BBP, et ${R_3NH^+}{(aq)}/{R_3N}_{(aq)}$ celui associé à la N,N-diméthylméthanamine.

Au cours du temps, les bactéries contenues dans le poisson produisent naturellement des molécules de N,N-diméthylméthanamine ${R_3N}{(aq)}$ qui entrent en contact avec la pastille imbibée de BBP.
La forme acide du BBP $BH{2(aq)}$ est de couleur jaune
$BH_{2(aq)}$ et ${R_3N}{(aq)}$ réagissent ensemble
$BH{2(aq)}+{R_3N}{(aq)}\rightleftarrows{{\rm BH}^-}{(aq)}+{R_3NH^+}_{(aq)}$

4.  Cinétique d’ordre 1 de la décoloration du BBP en présence d’ion hydroxyde

L’ion BH^– est une espèce amphotère. Les molécules de N,N-diméthylméthanamine produites lors de la dégradation du poisson rendent le milieu basique. En milieu très basique, le BBP se décolore selon une transformation chimique lente, considérée totale et modélisée par la réaction d’équation suivante :

BH^–(aq) + OH^–(aq) → B^2–(aq) + H2O(ℓ)

Q16. Justifier le caractère amphotère de l’ion BH^–.

${\rm BH}^-$ est la base du couple :
$BH_{2(aq)}/{{\rm BH}^-}{(aq)}$
L’équation de réaction :
${{\rm BH}^-}{(aq)}+{{\rm HO}^-}{(aq)}\rightarrow{B^{2-}}{(aq)}+H_2O(l)$
Montre que ${{\rm BH}^-}{(aq)}$ est capable de céder un proton H⁺ : c’est donc un acide.
${\rm BH}^-$ est l’acide du couple :
${{\rm BH}^-}{(aq)}/{B^{2-}}_{(aq)}$
Ainsi, ${\rm BH}^-$ est l’acide d’un couple et la base d’un autre : ${\rm BH}^-$ est une espèce amphotère.

On souhaite savoir si cette transformation peut nuire à l’efficacité d’un emballage intelligent.

Pour cela, on suit l’évolution de la concentration en ions BH^–, en fonction du temps, dans une solution très basique. Le protocole mis en place est le suivant :

• placer un volume d’une solution contenant des ions BH^– dans une fiole jaugée de 50,0 mL ;
• compléter jusqu’au trait de jauge avec une solution aqueuse d’hydroxyde de sodium introduite en excès ;
• suivre l’évolution de l’absorbance par spectrophotométrie pendant une trentaine de minutes et tracer l’évolution temporelle de la concentration en ions BH^–, notée [BH^–] (voir figure 4).

Figure 4. Évolution temporelle de la concentration en ions BH^–

Q17. Après avoir déterminé le temps de demi-réaction, indiquer si ce temps caractéristique et la réaction associée sont adaptés à une utilisation dans la pastille d’un emballage intelligent. Détailler votre raisonnement en explicitant les évolutions de la couleur de la pastille de l’emballage au cours du temps.

$t_{1/2}$ est la durée nécessaire pour que l’avancement atteigne la moitié de sa valeur finale : $x(t_{1/2}) = x_f/2$.
$\left[{\rm BH}^-\right]{\left(t=t{1/2}\right)}=\dfrac{\left[{\rm BH}^-\right]i}{2}$
$\left[{\rm BH}^-\right]{\left(t=t_{1/2}\right)}=\dfrac{5,6}{2}$
$\left[{\rm BH}^-\right]{\left(t=t{1/2}\right)}=2,8\ \mu mol.L^{-1}$

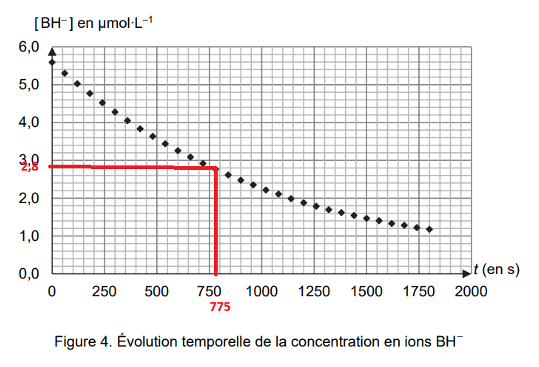
$t_{1/2}\approx 13\ min$ : il faut 13 min pour que la moitié des ions ${{\rm BH}^-}{(aq)}$, issus de la réaction avec la N,N-diméthylméthanamine, réagissent.
On considère qu’au bout de $5\ t{1/2}$, tous les ions ${{\rm BH}^-}{(aq)}$ ont réagi.
$5t{1/2}=5\times775=3875\ s\approx 1h$

D’après le sujet : « Au cours de la dégradation du poisson, qui se réalise sur plusieurs jours, la N,N-diméthylméthanamine, composé volatil, est produite. La pastille de BBP initialement jaune se colore alors en bleu. »
Cependant « en milieu très basique, le BBP se décolore … » en 1h.

Ainsi, après que le poisson se soit dégradé (réaction elle-même lente qui se déroule sur plusieurs jours), la pastille de BBP initialement jaune se colore alors en bleu, mais 1h plus tard, le BBP se décolore.

Le consommateur n’est pas constamment devant l’emballage, il ne verra certainement pas la pastille se colorer en bleu car 1h après elle devient incolore.

Ainsi, ce temps caractéristique et la réaction associée ne sont pas adaptés à une utilisation dans la pastille d’un emballage intelligent.