Vers la synthèse du plexiglas

Bac Métropole Juin 2021 Sujet 2

Exercice 1 – (10 points) –  Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée

Sujet n° 21-PYCJ2ME2

[latexpage]

Le polyméthacrylate de méthyle (PMMA) est un polymère thermoplastique transparent. Découvert en 1877, il

est produit industriellement dès 1933 en Allemagne à partir du méthacrylate de méthyle (MMA), sous le nom de Plexiglas®. Ce matériau permet de remplacer le verre pour certaines applications comme les écrans de protection par exemple.

L’objectif de cet exercice est d’étudier la synthèse du MMA, puis celle du PMMA.

Monomère	Polymère	Exemple d’objet fabriqué en plexiglas
Acronyme usuel : MMA Nom usuel : méthacrylate de méthyle Nomenclature officielle : 2-méthylpropénoate de méthyle Structure :	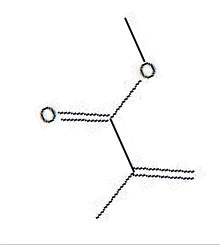Acronyme usuel : PMMA Nom usuel : polyméthacrylate de méthyle Nomenclature officielle : poly(2-méthylpropénoate de méthyle) Structure (partielle) :	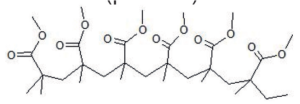Écran mobile de protection, en plexiglas

1. Étude de l’acide méthacrylique

L’acide méthacrylique peut être utilisé comme réactif dans la synthèse du MMA.

Données sur l’acide méthacrylique :

• nom dans la nomenclature officielle : acide 2-méthyl-2-propénoïque ;
• formule semi-développée :

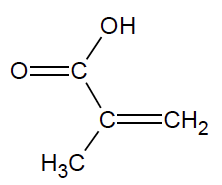
• masse molaire moléculaire : M = 86,1 g·mol–1 ;
• pKA, à 25°C, du couple acide méthacrylique / ion méthacrylate : 4,7 ;

Source : d’après www.merckgroup.com

1.1. Indiquer les précautions opératoires et les équipements de sécurité nécessaires à la manipulation de l’acide méthacrylique. Justifier.

Mentions de danger de l’acide méthacrylique :

• Nocif en cas d’ingestion ou d’inhalation.
• Toxique par contact cutané.
• Provoque des brûlures de la peau et de graves lésions des yeux.
• Peut irriter les voies respiratoires.

Il faut donc porter une blouse, des gants et des lunettes de protection. Nous devons également travailler sous hotte aspirante.

1.2. Représenter, sur votre copie, la formule topologique de l’acide méthacrylique et entourer les groupes caractéristiques.

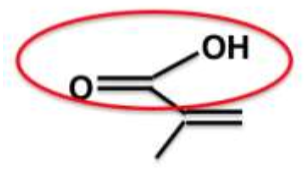
1.3. Justifier que la molécule d’acide méthacrylique est un acide au sens de Brönsted et écrire le couple acide- base associé.

L’acide méthacrylique possède un group carboxyle COOH, il est capable de céder un proton H+ : c’est un acide au sens de Brönsted.

Couple acide base associé : C₄H₆O₂/C₄H₅O^–

1.4. Écrire l’équation de la réaction de l’acide méthacrylique, noté HA, dans l’eau.

$$AH_{(aq)} + H_2O_{(l)} \rightleftharpoons A^-{(aq)} + H_3O^+{(aq)}$$

1.5. Donner la relation entre la constante d’acidité KA du couple acide méthacrylique / ion méthacrylate noté HA / A^– et les concentrations en quantité de matière à l’équilibre des espèces chimiques HA et A^–.

$$K_a = \frac{[A^-]{eq} \times [\mathrm{H_3O^+}]{eq}}{[HA]_{eq} \times c_0}$$

1.6. Vérifier, par un raisonnement quantitatif, que la valeur du pH d’une solution aqueuse d’acide méthacrylique de concentration c_m = 100 g·L^–1 est de 2,3.

$$pH=-log\left(\frac{\left[H_3O^+\right]}{c^0}\right)$$

Il nous faut trouver $\left[H_3O^+\right]$, connaissant $C_m$ et pKa.

Construisons un tableau d’avancement :

	AH	H2O     ⇄	A−	H3O+
Etat initial	CV	Solvant	0	0
Etat intermédiaire	CV−x	Solvant	x	x
Etat final	CV−xf	Solvant	xf	xf

Exprimons Ka en fonction de $\left[H_3O^+\right]$ et c.

D’après le tableau d’avancement :

$$n_{H_3O^+}^f = x_f $$
$$\left[ H_3O^+ \right]{eq} = \frac{n{H_3O^+}^f}{V} = \frac{x_f}{V} $$

$$n_{A^-}^f = x_f $$
$$\left[ A^- \right]{eq} = \frac{n{A^-}^f}{V} = \frac{x_f}{V} = \left[ H_3O^+ \right]_{eq} $$

$$n_{AH}^f = C \times V – x_f $$
$$\left[ HA \right]{eq} = \frac{n{AH}^f}{V} = \frac{C \times V – x_f}{V} = C – \frac{x_f}{V} = C – \left[ H_3O^+ \right]_{eq} $$

Donc
$$K_a = \frac{[A^-]{eq} \times [H_3O^+]{eq}}{[HA]{eq} \times c^0} $$

$$K_a = \frac{\left[ H_3O^+ \right]{eq} \times \left[ H_3O^+ \right]{eq}}{\left( C – \left[ H_3O^+ \right]{eq} \right) \times c^0}$$

$$K_a = \frac{\left[ H_3O^+ \right]{eq}^2}{\left( C – \left[ H_3O^+ \right]{eq} \right) \times c^0}$$

Remplaçons dans cette équation Ka et C par leur valeurs :

$$K_a = 10^{-pK_a} = 10^{-4,7} = 2{,}0 \times 10^{-5} $$

$$ C = \frac{C_m}{M} = \frac{100}{86,1} = 1{,}16\ \text{mol·L}^{-1} $$

$$c^0 = 1{,}0\ \text{mol·L}^{-1} $$

$$K_a = \frac{[\mathrm{H_3O^+}]{eq}^2}{(C – [\mathrm{H_3O^+}]{eq}) \times c^0}$$

$$2{,}0 \times 10^{-5} = \frac{[\mathrm{H_3O^+}]{eq}^2}{(1{,}16 – [\mathrm{H_3O^+}]{eq}) \times 1{,}0} $$

$$\text{Trouvons } [\mathrm{H_3O^+}]_{eq} : $$

$$ 2{,}0 \times 10^{-5} (1{,}16 – [\mathrm{H_3O^+}]{eq}) = [\mathrm{H_3O^+}]{eq}^2$$

$$ 2{,}32 \times 10^{-5} – 2{,}0 \times 10^{-5} [\mathrm{H_3O^+}]{eq} = [\mathrm{H_3O^+}]{eq}^2 $$

$$ [\mathrm{H_3O^+}]{eq}^2 + 2{,}0 \times 10^{-5} [\mathrm{H_3O^+}]{eq} – 2{,}32 \times 10^{-5} = 0 $$

Nous obtenons une équation du second degré :

$$
\Delta = b^2 – 4ac
$$
$$
\Delta = (2{,}0\times10^{-5})^2 – 4\times1\times(-2{,}32\times10^{-5})
$$
$$
\Delta = 9{,}28\times10^{-5}
$$

$$[\mathrm{H_3O^+}]{eq} = \frac{-b \pm \sqrt{\Delta}}{2a} $$

$$ [\mathrm{H_3O^+}]{eq} = \frac{-2{,}0\times10^{-5} \pm \sqrt{9{,}28\times10^{-5}}}{2} $$
$$[\mathrm{H_3O^+}]{eq} = 4{,}8\times10^{-3}\ \text{mol·L}^{-1} $$

$$
[\mathrm{H_3O^+}]_{eq} = \frac{-b – \sqrt{\Delta}}{2a}
$$

$$[\mathrm{H_3O^+}]_{eq} = \frac{-2{,}0\times10^{-5} – \sqrt{9{,}28\times10^{-5}}}{2\times1}
$$

$$[\mathrm{H_3O^+}]_{eq} = -4{,}8\times10^{-3}\ \text{mol·L}^{-1}$$

Nous ne gardons que la valeur positive :
$$[\mathrm{H_3O^+}]{eq} = 4{,}8\times10^{-3}\ \text{mol·L}^{-1} $$

$$
\mathrm{pH} = -\log\left(\frac{[\mathrm{H_3O^+}]}{c^0}\right)
$$
$$
\mathrm{pH} = -\log\left(\frac{4{,}8\times10^{-3}}{1{,}0}\right) = 2{,}3
$$

La valeur est en accord avec celle annoncée.

2. Synthèse du monomère : le méthacrylate de méthyle (MMA)

Le méthacrylate de méthyle est un ester qui peut être préparé au laboratoire par réaction entre l’acide méthacrylique et le méthanol. Cette transformation est très lente en l’absence de catalyseur et n’est pas totale. Un protocole opératoire possible est décrit ci-dessous.

Étape a. Dans le respect des consignes de sécurité, placer 10,0 g d’acide méthacrylique dans un ballon de 100 mL. Ajouter 35 mL de méthanol puis introduire goutte à goutte 2 mL d’acide sulfurique concentré. Adapter un réfrigérant puis porter le mélange réactionnel au reflux pendant 30 minutes en agitant.

Étape b. Refroidir le milieu réactionnel puis le verser dans 50 mL d’eau glacée. Transvaser le tout dans une ampoule à décanter et procéder à deux extractions successives avec 25 mL d’éther diéthylique. Rassembler les phases organiques puis les laver avec, successivement, 30 mL d’eau glacée, 50 mL d’une solution d’hydrogénocarbonate de sodium à 5% puis 30 mL d’une solution saturée de chlorure de sodium. Sécher la phase organique sur sulfate de magnésium anhydre.

Étape c. Mettre en place un montage de distillation fractionnée. Récupérer la fraction distillée correspondant au MMA et mesurer la masse du liquide obtenu.

Données :

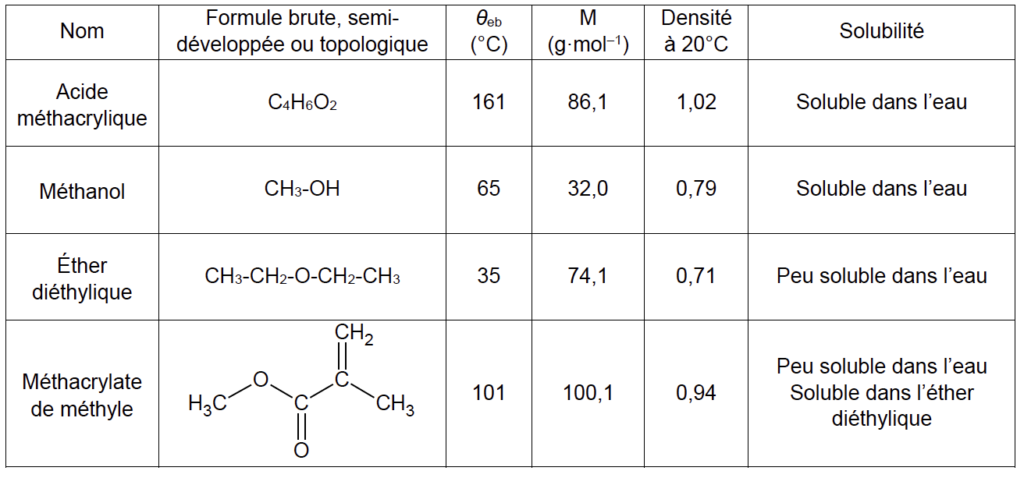
2.1. Réaliser un schéma légendé du montage à reflux utilisé dans l’étape a et proposer un nom pour cette étape du protocole.

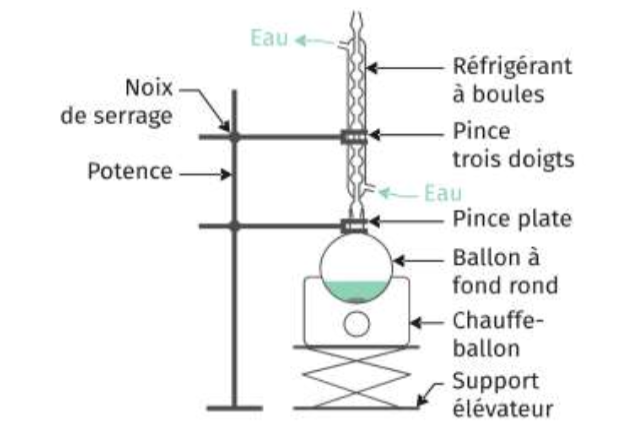
2.2. Établir l’équation de la réaction modélisant la synthèse, sachant que de l’eau est produite au cours de cette transformation.

D’après le texte : « Le méthacrylate de méthyle est un ester qui peut être préparé au laboratoire par réaction entre l’acide méthacrylique et le méthanol » … « Sachant que de l’eau est produite au cours de cette transformation. »

Réactifs :

Acide méthacrylique  C₄H₆O₂

Méthanol CH₄O

Produits :

Méthacrylate de méthyle C₅H₈O₂

Eau H₂O

$$
\mathrm{C_4H_6O_2} + \mathrm{CH_4O} \rightleftharpoons \mathrm{C_5H_8O_2} + \mathrm{H_2O}
$$

2.3. Justifier les positions relatives des phases organique et aqueuse lors du lavage à l’eau glacée, dans l’ampoule à décanter, lors de l’étape b. Préciser la composition de chaque phase.

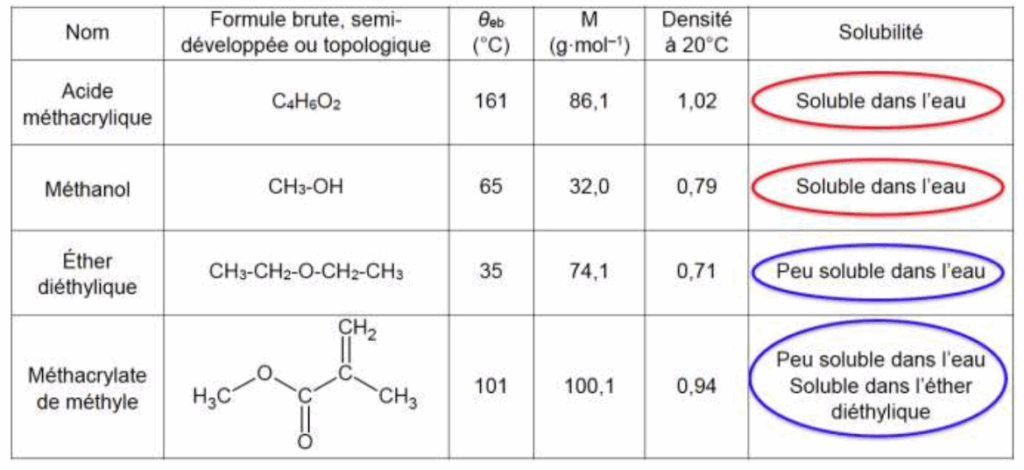
Phase aqueuse : eau d=1,00	Phase organique : Éther diéthylique d=0,71
Eau Acide méthacrylique Méthanol	Éther diéthylique Méthacrylate de méthyle

d_{Éther diéthylique}< d_eau , la phase organique est au-dessus de la phase aqueuse.

2.4. Donner le rôle de l’étape c, et indiquer ce qui doit être surveillé pour être sûr de récupérer le MMA lors de la distillation fractionnée.

Étape c. Mettre en place un montage de distillation fractionnée

La distillation fractionnée permet de séparer les constituants d’un mélange qui ont des températures d’ébullition différences.

Ainsi l’étape c permet de séparer l’éther diéthylique et le méthacrylate de méthyle.

$\theta_{eb}éther diéthylique=35°C$ et $\theta_{eb}méthacrylate de méthyle=101°C$

Il faut surveiller la température pour être sûr de récupérer le MMA. Dés que la température atteint 100,1°C , on arrête de chauffer et on récupère le MMA dans le ballon.

2.5. Déterminer les quantités de matière des réactifs introduits.

$$n_{\text{acide méthacrylique}} = \frac{m_{\text{acide méthacrylique}}}{M_{\text{acide méthacrylique}}}
$$
$$
n_{\text{acide méthacrylique}} = \frac{10,0}{86,1}
$$
$$
n_{\text{acide méthacrylique}} = 1,16\times10^{-1}\ \text{mol}
$$

$$
n_{\text{méthanol}} = \frac{m_{\text{méthanol}}}{M_{\text{méthanol}}}
$$
$$
\text{Or } \rho_{\text{méthanol}} = \frac{m_{\text{méthanol}}}{V_{\text{méthanol}}}
$$
$$
n_{\text{méthanol}} = \frac{\rho_{\text{méthanol}} \times V_{\text{méthanol}}}{M_{\text{méthanol}}}
$$

Or
$$
d_{\text{méthanol}} = \frac{\rho_{\text{méthanol}}}{\rho_{\text{eau}}}
$$
$$
n_{\text{méthanol}} = \frac{d_{\text{méthanol}} \times \rho_{\text{eau}} \times V_{\text{méthanol}}}{M_{\text{méthanol}}}
$$
$$
n_{\text{méthanol}} = \frac{0,79\times1000\times35\times10^{-3}}{32,0}
$$

$$
n_{\text{méthanol}} = 8,6\times10^{-1}\ \text{mol}
$$

2.6. En supposant la transformation totale, déterminer la masse maximale de méthacrylate de méthyle qui peut être obtenue.

$$
x_{max1} = n_{\text{acide méthacrylique}} = 1,16\times10^{-1}\ \text{mol}
$$
$$
x_{max2} = n_{\text{méthanol}} = 8,6\times10^{-1}\ \text{mol}
$$

$$
x_{max1} < x_{max2}
$$
$$
x_{max} = 1,16\times10^{-1}\ \text{mol}
$$

Masse maximale de méthacrylate de méthyle qui peut être obtenue :

$$
m_{\text{Méthacrylate de méthyle}} = n_{\text{Méthacrylate de méthyle}} \times M_{\text{Méthacrylate de méthyle}}
$$
$$
m_{\text{Méthacrylate de méthyle}} = x_{max} \times M_{\text{Méthacrylate de méthyle}}
$$
$$
m_{\text{Méthacrylate de méthyle}} = 1,16\times10^{-1} \times 100,1
$$
$$
m_{\text{Méthacrylate de méthyle}} = 11,6\ \text{g}
$$

2.7. Indiquer une méthode mise en œuvre pour optimiser la vitesse d’apparition du MMA et une méthode mise en œuvre pour optimiser le rendement de cette synthèse.

Méthode mise en œuvre pour optimiser la vitesse d’apparition du MMA : le chauffage à reflux et présence d’acide sulfurique (catalyseur).

Méthode mise en œuvre pour optimiser le rendement de cette synthèse : on a introduit un des réactifs en excès (le méthanol).

3. Synthèse et propriétés du polymère : le polyméthacrylate de méthyle (PMMA)

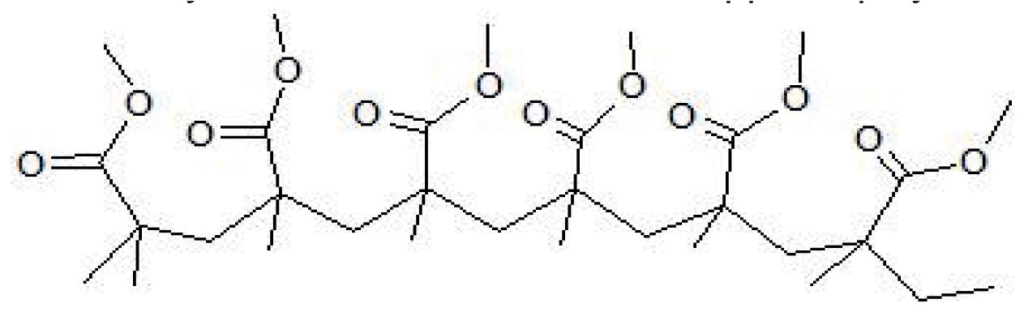
Le polyméthacrylate de méthyle est une macromolécule linéaire (voir figure 1) produite par transformation chimique du méthacrylate de méthyle. Cette transformation est appelée polymérisation.

Données :

• bandes d’absorption en spectroscopie infrarouge (IR) :

Liaison	O – H (acide carboxylique)	Ctét – H	C = O	C = C	Ctét – O
Nombre d’onde σ (cm–1)	2500 – 3200	2800 – 3000	1650 – 1750	1620 – 1690	1050 – 1450

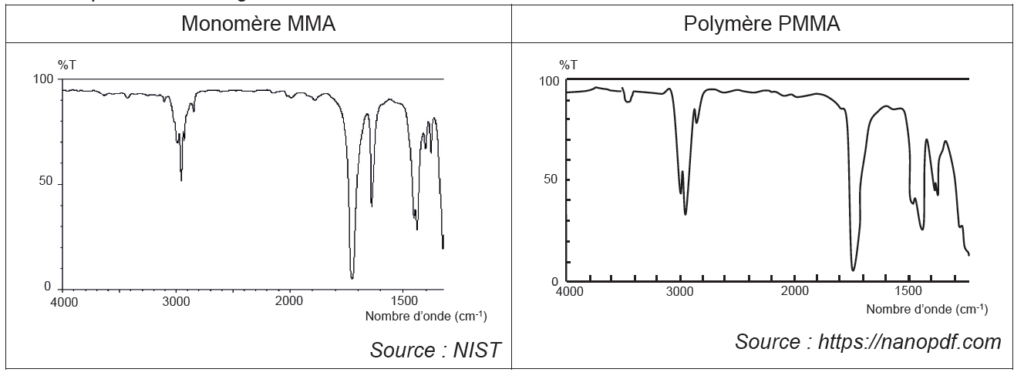
• spectres infrarouge :

3.1. Représenter le motif du polymère.

3.2. Justifier que l’on puisse suivre la transformation par spectroscopie infrarouge.

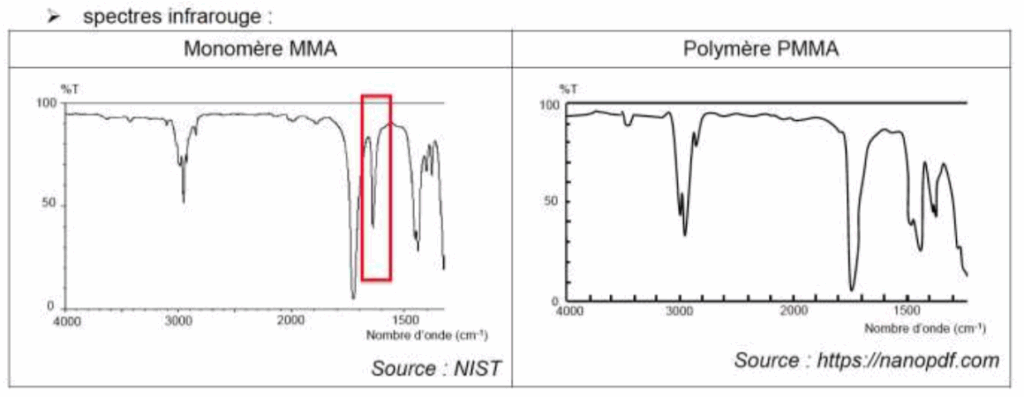
Une différence existe entre ces 2 spectres : une bande vers 1650 cm^-1 disparait lors de la formation du polymère. On peut donc suivre la transformation par spectroscopie infrarouge.

Parmi les procédés industriellement mis en œuvre, l’un permet des conditions douces respectueuses de l’environnement et des vitesses relativement élevées. L’étude cinétique de la figure 2 présente des résultats expérimentaux obtenus dans les conditions opératoires optimales pour contrôler la synthèse, c’est-à-dire pour obtenir des chaines de polymères de grandes longueurs et de tailles homogènes. La vitesse volumique de disparition du monomère MMA est notée v_p.

Temps (h)	[MMA] (mmol·L–1)	vp (mmol·L–1·h-1)
0	518	vp,0
1	311	188
2	123	55,0
3	68,0	25,0
4	43,0	20,1
5	22,9	8,50
6	14,4

Figure 2. Résultats expérimentaux. Source : D’après ACS Macro Letters

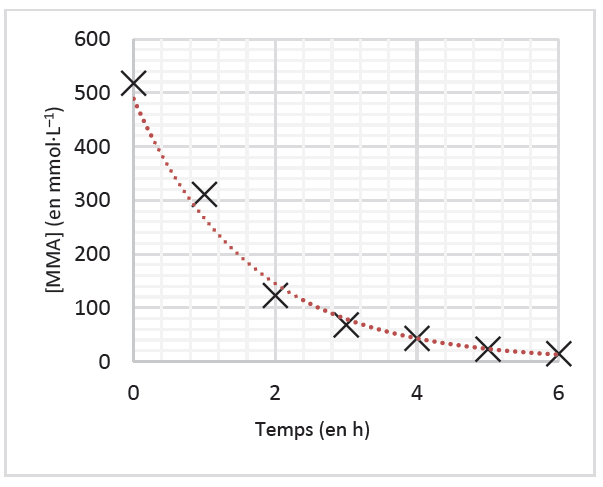
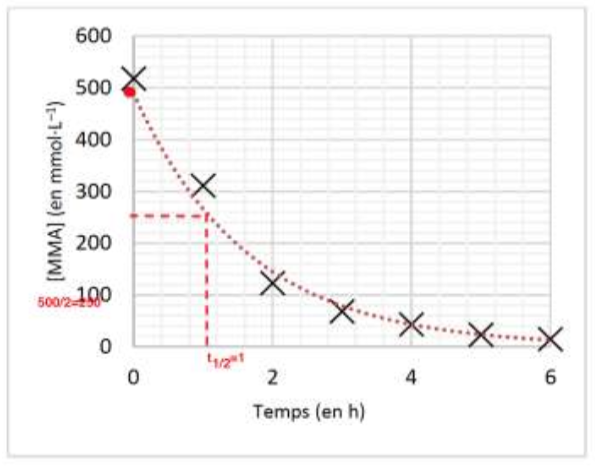
3.3. Déterminer le temps de demi-réaction t_1/2 de la polymérisation du MMA à l’aide de la figure 3. Commenter.

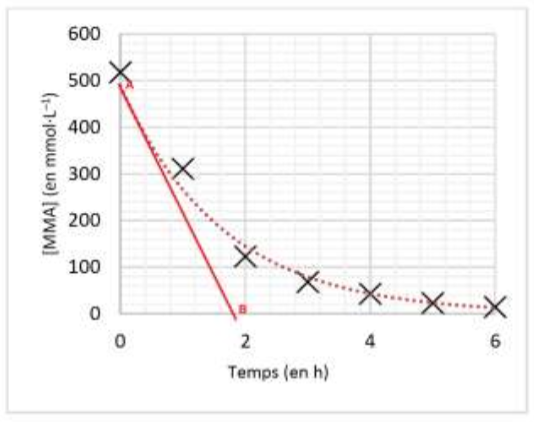
3.4. À l’aide de la figure 3, estimer en explicitant la méthode, la valeur de la vitesse de disparition vp de MMA à l’instant initial.

$$v_d=-\frac{d\left[MMA\right]_{(t)}}{dt}$$

La dérivée se calcul en trouvant le coefficient directeur de la tangente en un point de la courbe.

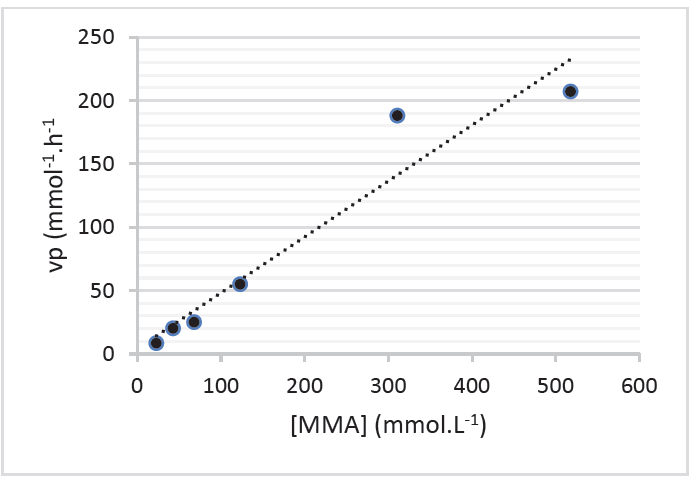
3.5. En étudiant l’évolution de la vitesse v_p en fonction de la concentration en MMA sur la figure 4, déterminer si l’évolution temporelle de la concentration en MMA suit une loi de vitesse d’ordre 1.

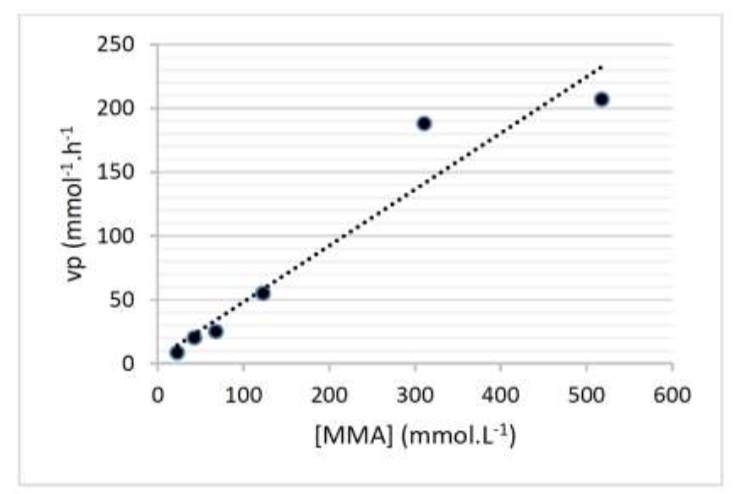
Nous avons une droite qui passe par l’origine donc  $v_d$ est proportionnel à $\left[MMA\right]_{(t)} : \ v_d=k \times \left[MMA\right]_{(t)}$

C’est bien en accord avec une loi de vitesse d’ordre 1.