E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02709
Télécharger l’exercice en PDF :
Les séismes sont des événements redoutés par l’espèce humaine car ils sont associés à des destructions massives et imprévisibles. Pourtant un réseau de surveillance existe et détecte à l’échelle planétaire les vibrations du sol dont la plupart sont inoffensives.
L’objectif de cet exercice est de comprendre comment on peut localiser l’épicentre d’un séisme. Pour répondre à cette question, il faut d’abord s’intéresser aux ondes de différentes natures responsables des secousses sismiques.
Nature des ondes sismiques
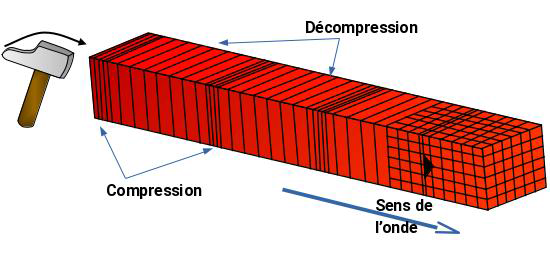
Les ondes P sont aussi appelées ondes longitudinales. La vibration du sol se fait par des dilatations et des compressions successives. Ces perturbations se déplacent parallèlement à la direction de propagation de l’onde. Les ondes P se propagent dans les milieux solides ainsi que dans les liquides.
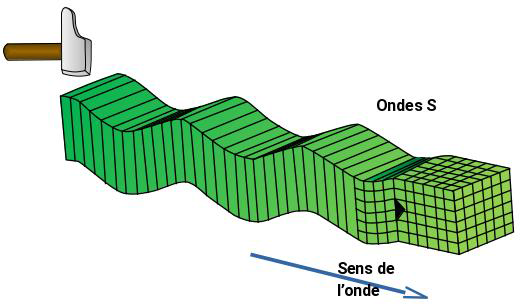
Les ondes S sont aussi appelées ondes transversales. À leur passage, les perturbations du sol s’effectuent perpendiculairement au sens de propagation de l’onde. Les ondes S ne se propagent que dans les milieux solides.
1. Les ondes P et S sont qualifiées d’ondes de typemécanique. Justifier cette affirmation.
On appel onde mécanique progressive, le phénomène de propagation d’une perturbation dans un milieu matériel sans transport de matière, mais avec transport d’énergie.
Les ondes P se propagent dans les milieux solides ainsi que dans les liquides.
Les ondes S ne se propagent que dans les milieux solides.
Ces deux ondes ne se propagent pas dans le vide : ce sont des ondes mécaniques.
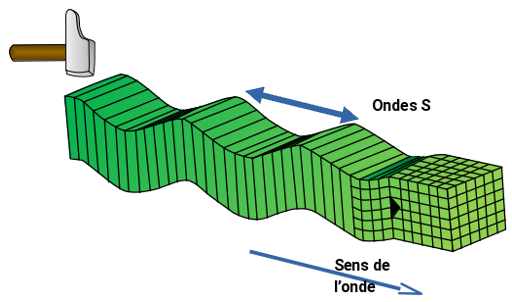
2. On considère ces ondes comme périodiques. Indiquer quelle est la grandeur représentée par la flèche double en pointillés sur la représentation précédente des ondes S.
La grandeur représentée entre deux maximum est la longueur d’onde λ.
(d’après données planet-terre.ens-lyon.fr)
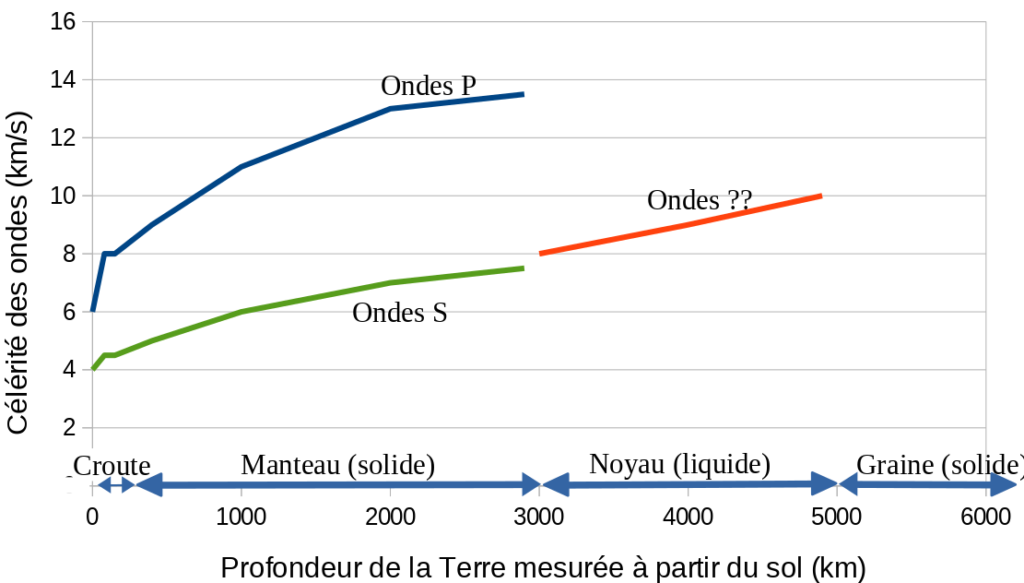
3. Indiquer quel est le type d’onde (P ou S) qui traverse le noyau terrestre. Justifier.
Le noyau terrestre est liquide . Seul les ondes P se propagent dans les milieux dans les liquides.
Ce sont donc les ondes P qui traversent le noyau terrestre.
Détection des séismes
Lorsqu’un séisme se produit, les ondes sismiques ne sont pas forcément détectées par l’être humain, mais elles peuvent être suivies par les nombreux sismographes situés sur la Terre dans des stations de surveillance sismique.
Un sismographe traditionnel est constitué d’un bâti fixe et d’un pendule qui réagit aux secousses. Le dispositif permet de transcrire les secousses enregistrées sous forme d’une courbe tracée si le mécanisme est mécanique, ou sous forme de données informatiques pour les sismographes numériques modernes.
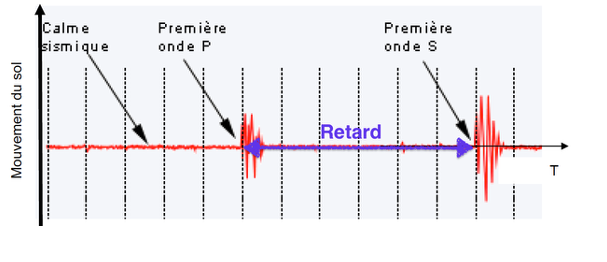
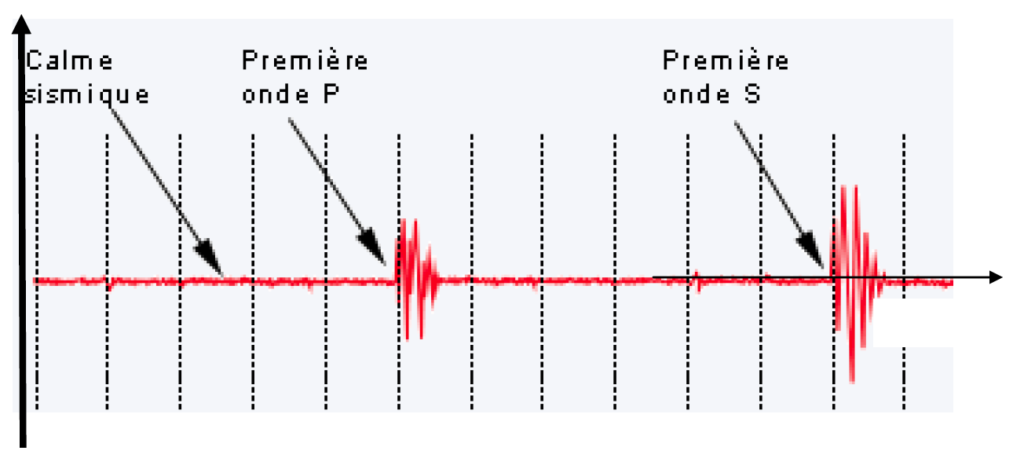
Ces sismographes permettent d’obtenir des sismogrammes qui peuvent être décomposés comme sur le document en annexe 1 à rendre avec la copie.
4. Déterminer si l’allure du sismogramme fourni (annexe 1) est cohérente avec les informations du graphe précédent.
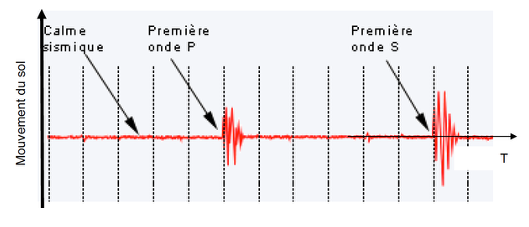
Les ondes P sont perçus avant les ondes S. C’est cohérent avec les informations du graphe précédent qui indique que les ondes P sont plus rapides que les ondes S.
5. Représenter sur le document donné en annexe 1 à rendre avec la copie, le retard de l’onde S par rapport à l’onde P.
Localisation de l’épicentre
Un séisme se produit généralement à l’intérieur du globe terrestre. L’épicentre du séisme est le lieu de la surface, le plus proche de la source du séisme. C’est le premier endroit de la surface à recevoir les ondes sismiques.
Un séisme dont l’épicentre se situe en Équateur, pays d’Amérique du Sud, s’est produit le 22 février 2019. L’enregistrement du sismographe de la station de surveillance LFCV située au Venezuela, un autre pays d’Amérique du Sud, a permis de mesurer les heures d’arrivée des ondes P et S.
On fera les hypothèses suivantes pour modéliser simplement la situation :
- hypothèse 1 : les ondes P et S se propagent quasiment à la surface de la Terre ;
- hypothèse 2 : le rayon de courbure de la Terre est négligeable ;
- hypothèse 3 : les ondes se déplacent avec des célérités de valeurs constantes.
Données :
| Type d’onde | Heure d’arrivée à la station LFCV | Célérités moyennes des ondes | Distance parcourue depuis l’épicentre |
| Ondes P | HP = 10 h 21 min 01 s | cP = 8,7 km.s-1 | d |
| Ondes S | HS = 10 h 24 min 03 s | cS = 4,7 km.s-1 | d |
6. On note d la distance entre l’épicentre du séisme et la station LFCV. En notant tS et tP respectivement les durées de propagation de l’onde S et de l’onde P entre l’épicentre et la station LFCV, exprimer tS – tP en fonction de d, cS et cP.
$v=c=\frac{d}{t}$
d’ou
$t=\frac{d}{c}$
$t_S-t_P=\frac{d}{c_S}-\frac{d}{c_P}=d\left(\frac{1}{c_S}-\frac{1}{c_P}\right)$
7. Exprimer la distance d puis calculer sa valeur.
$$d=\frac{t_S-t_P}{\left(\frac{1}{c_S}-\frac{1}{c_P}\right)}$$
$t_S-t_P=10\ h\ 24\min\ 03\ s-\ 10\ h\ 21\min\ 01\ s=3\min\ 02\ s=3\times60+02=182\ s$
$$d=\frac{182}{\left(\frac{1}{4,7}-\frac{1}{8,7}\right)}=1,9.10^3km$$
En réalité, les calculs de localisation d’épicentre prennent en compte le fait que les célérités des ondes P et S ne sont pas constantes. On réalise pour cela une hodochrone (voir ci-dessous) à partir des enregistrements obtenus par plusieurs sismographes situés en divers endroits du globe. Elle représente l’évolution du temps de propagation des ondes sismiques P et S en fonction de la distance à l’épicentre.
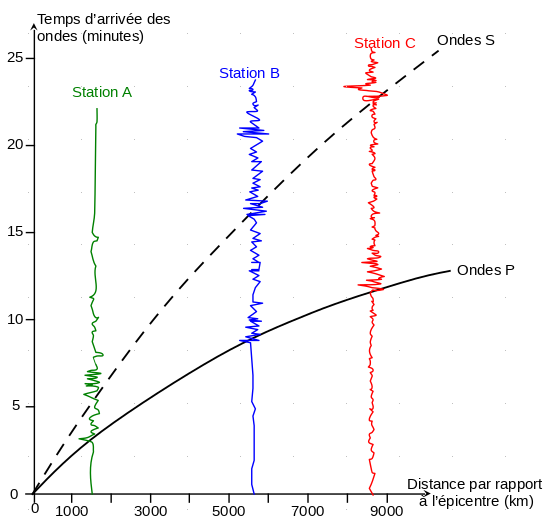
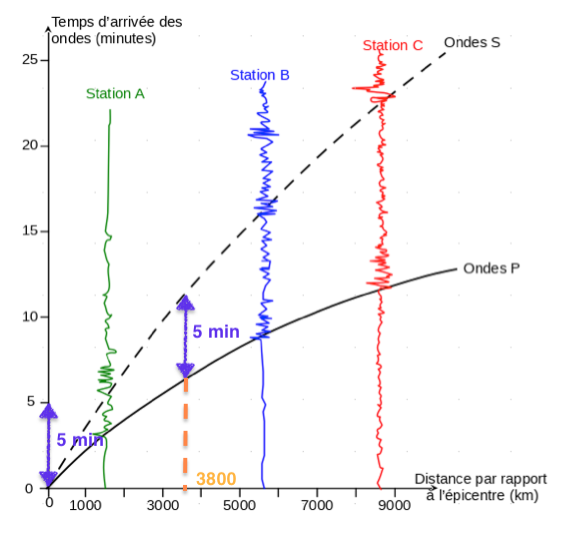
8. En exploitant l’hodochrone, déterminer la distance L entre l’épicentre et une station de mesure dans le cas où l’onde S arrive avec 5 min de retard par rapport à l’onde P.
S arrive avec 5 min de retard par rapport à l’onde P.
Il faut lire sur le graphique la distance correspondant à un retard entre les ondes S et P de 5 min.
L=3800 km
L’utilisation de l’hodochrone donne pour trois stations différentes les résultats suivants :
| Station | Durée tS-tp | Distance L de la station à l’épicentre |
| LFCV (Venezuela) | 183 s | 1,93.103 km |
| HPAP (Haïti) | 231 s | 2,39.103 km |
| GCAPE (Guadeloupe) | 247 s | 2,78.103 km |
On considère que, pour chaque station, l’épicentre se trouve sur un cercle de rayon L.
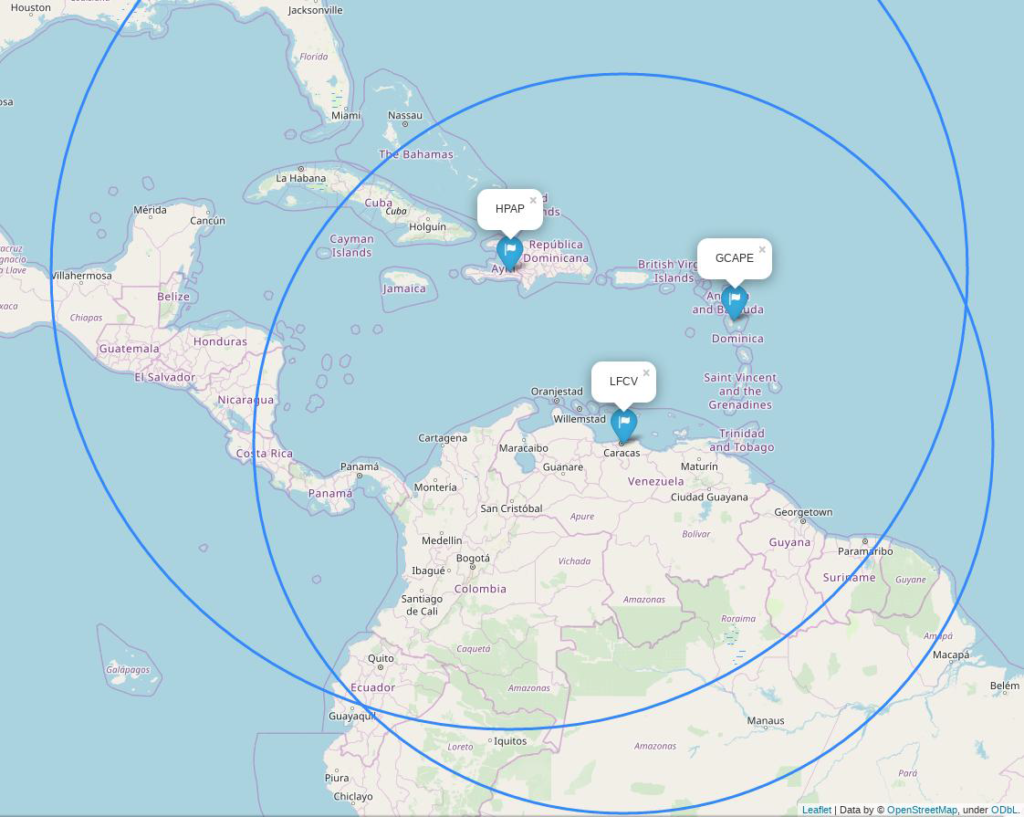
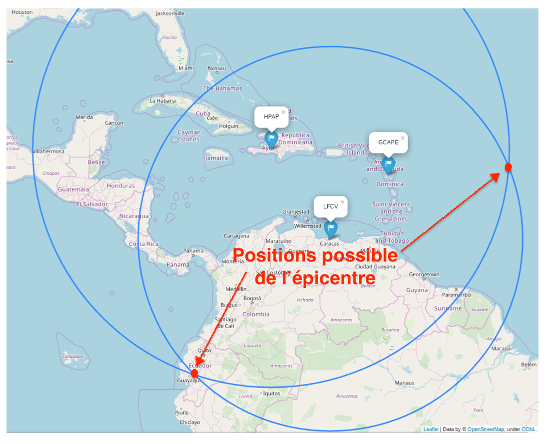
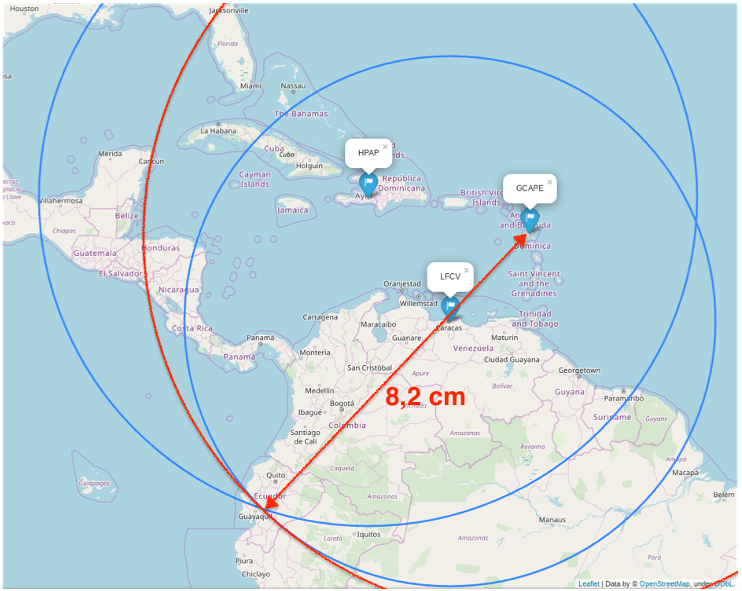
Pour déterminer graphiquement la position de l’épicentre, on a utilisé un programme informatique en langage Python. Ce programme permet de créer un fond de carte, de positionner les trois stations LFCV, HPAP et GCAPE, de tracer des cercles dont les centres sont les stations. La carte produite figure dans le document en annexe 2 à rendre avec la copie.
9. Indiquer pourquoi le document en annexe 2 à rendre avec la copie ne permet pas de positionner précisément l’épicentre du séisme.
L’épicentre du séisme se situe à l’intersection des cercles autour des stations. Cependant il existe 2 positions possible de l’épicentre sur ce document.
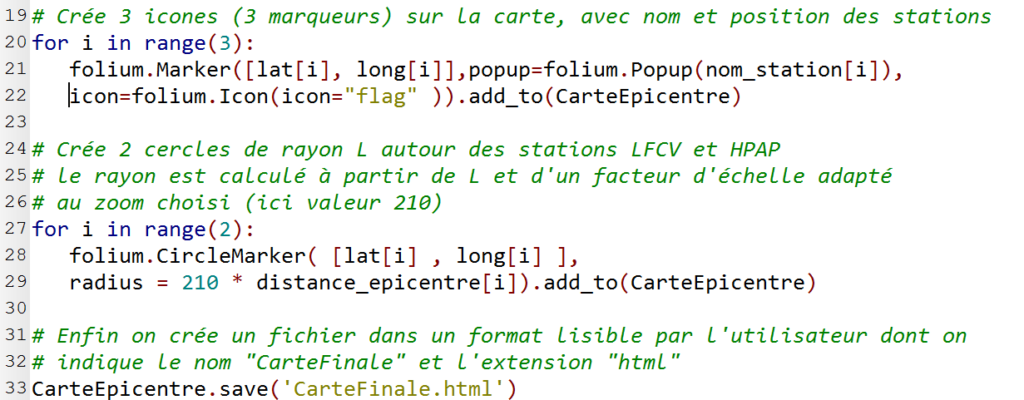
Le programme utilisé est donné ci-dessous :
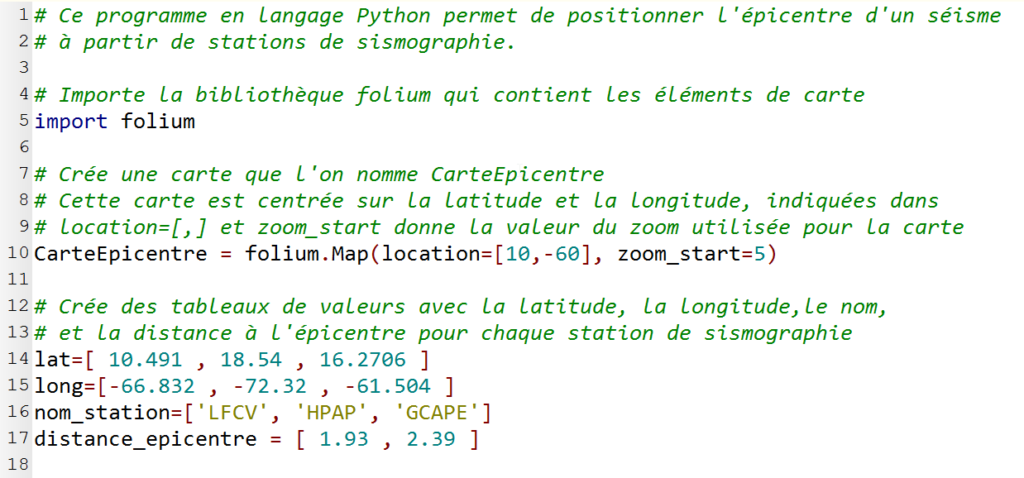
10. Indiquer l’information chiffrée manquante dans ce programme informatique, pour tracer le cercle autour de la station GCAPE. Préciser le numéro de la ligne à corriger et réécrire cette ligne entièrement sur votre copie.
Il y a 3 stations : LFCV, HPAP et GCAPE (voir carte de l’annexe)
Ligne 17 : la distance entre les stations et l’épicentre. On remarque qu’il y a 2 valeurs au lieu des 3 valeurs attendues (une valeur par station). Il manque la distance pour GCAPE : L=2,78.10^3 km.
Réécriture de la ligne :
Ligne 17 : distance_epicentre = [1.93 , 2.39 , 2.78]
11. À la ligne 27, proposer une modification du programme permettant de faire apparaître le cercle autour de GCAPE.
A la ligne 27 : for i in range(2) , i ne prend que 2 valeurs et donc crée 2 cercles.
Pour faire apparaître le cercle autour de GCAPE, il faut écrire :
ligne 27 : for i in range(3)
12. Placer l’épicentre sur l’annexe 2 à rendre avec la copie en expliquant votre démarche.
Pour placer l’épicentre, il faut tracer le 3ème cercle autour de GCAPE de rayon L=2,78.103 km.
Trouvons l’échelle de ce document :
Nous savons que le cercle autour de LFCV est de rayon 1,93.103 km. Nous mesurons sur le schéma 5,7 cm.
| Distance réelle | A l’échelle | |
| LFCV | 1,93.103 km | 5,7 cm |
| GCAPE | 2,78.103 | x |
$x=\frac{2,78.10^3\times5,7}{1,93.10^3}=8,2cm$
Il faut donc tracer un cercle de centre GCAPE de rayon 8,2 cm.
ANNEXES À RENDRE AVEC LA COPIE
Annexe 1: Enregistrement simplifié des mouvements du sol en fonction du temps lors d’un séisme
Annexe 2 : Carte obtenue par le programme en langage python