E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02688, n°G1SPHCH02695, n°G1SPHCH02723 et n°G1SPHCH02733
Télécharger l’exercice en PDF :
En chimie, une végétation métallique est un type de dendrites produites par certaines transformations chimiques. La découverte de ces « feuillages métalliques » est attribuée à des alchimistes au Moyen-Age, qui croyaient y voir un phénomène magique. L’alchimie, malgré son statut de pseudoscience (c’est à dire de « fausse » science), a eu un rôle important dans le développement, au cours du XVIIIe siècle, de la chimie en tant que discipline scientifique s’appuyant sur des faits expérimentaux.
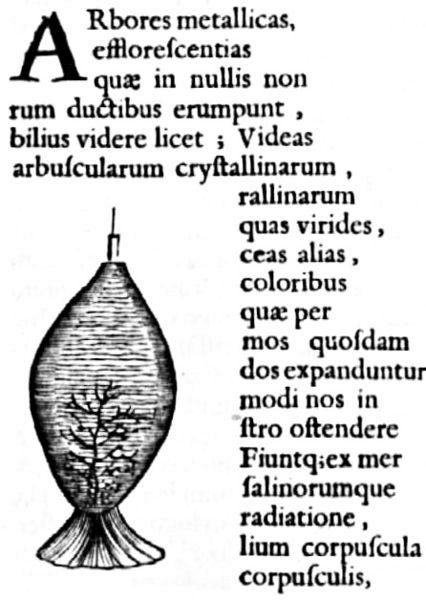

Figure 1. Un des premières publications d’une végétation chimique par Athanase Kircher, dans Mundus subterraneus en 1660 (d’après : wikipedia.org/Athanasius-Kircher-Mundus-subterraneus.jpg)
On s’intéresse dans cet exercice à la modélisation du phénomène de « végétations métalliques » à l’aide des outils de la chimie moderne, en s’interrogeant notamment sur la nature de ce métal qui se dépose comme les feuilles d’un arbre.
Données :
- Couples oxydant/réducteur
- couple ion argent/argent : Ag+/Ag ;
- couple ion cuivre/cuivre : Cu2+/Cu.
- Couleurs des solutions aqueuses :
- les ions cuivre Cu2+(aq) donnent une couleur bleue aux solutions aqueuses ;
- les ions argent Ag+(aq) et les ions nitrate NO3–(aq) sont incolores en solution aqueuse.
- Masses molaires atomiques :
M(Cu) = 63,5 g/mol, M(O) = 16,0 g/mol, M(Ag) = 107,9 g/mol,
M(N) = 14,0 g/mol.
- Électronégativités selon l’échelle de Pauling : O : 3,2 , C : 2,6 , H : 2,2.
Les alchimistes décrivent l’arbre de Diane comme une végétation d’argent se déposant sur un tronc fait en cuivre.
On souhaite fabriquer un arbre de Diane au laboratoire. Pour ce faire, on place un fil de cuivre, de masse initiale m’ = 5,6 g dans un bécher contenant V = 220 mL d’une solution de nitrate d’argent à la concentration en quantité de matière égale à c = 0,10 mol.L-1.
1. Préparation de la solution métallique pour réaliser l’arbre de Diane
Pour les chimistes, l’eau est un solvant très utilisé. Ses propriétés sont utilisées dans la réalisation de la végétation métallique car l’eau est capable de dissoudre le nitrate d’argent AgNO3 (s) et les autres ions intervenant dans le phénomène.
1.1. Donner le schéma de Lewis d’une molécule d’eau, justifier sa forme coudée et indiquer ses propriétés en lien avec les électronégativités des atomes qui la constituent.
Schéma de Lewis d’une molécule d’eau
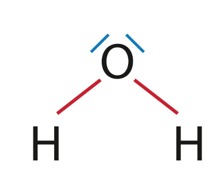
Il y a 2 doublets liants et 2 doublets non liants autour de l’atome central.
Ces doublets se disposent de autour de l’atome central afin que la répulsion entre les doublets soit minimale. Cependant la répulsion entre les entre les doublets non liants étant plus importante que la répulsion entre les doublets liants. C’est pourquoi la géométrie de la molécule d’eau est coudée.
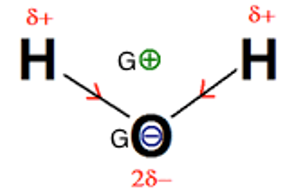
χO> χH Les liaisons OH sont polarisés.
Le barycentre (centre géométrique) des charges positives G+ est différent du barycentre des charges négatives G-.
La molécule est donc polaire
1.2. Écrire l’équation de la réaction modélisant la dissolution du nitrate d’argent dans l’eau. Préciser l’état physique des différentes espèces chimiques.
$AgNO_3\ (s)\rightarrow Ag^+\ (aq)+NO_3^-\ (aq)$
1.3. On note c la concentration en quantité de matière apportée en nitrate d’argent dans une solution. Exprimer, en fonction de c, la concentration en ions argent dissous [Ag+], si la dissolution est totale.
Si la dissolution est totale :
$[Ag^+(aq)]=c$
1.4. En déduire la quantité de matière n d’ions argent Ag+ contenue dans 250 mL de la solution de nitrate d’argent de concentration c = 0,10 mol.L-1 et indiquer la masse m de nitrate d’argent nécessaire pour préparer cette solution.
$[Ag^+(aq)]=c$
$\frac{n_{Ag^+}}{V}=c$
$n_{Ag^+}=c\times V$
$n_{Ag^+}=0,1\times250.10^{-3}=2,5.10^{-2}\ mol$
$m_{AgNO_3}=n_{AgNO_3}\times M_{AgNO_3}$
$m_{AgNO_3}=c\times V\times M_{AgNO_3}=0,1\times250.10^{-3}\times(107,9+14,0+3\times16,0)=4,2g$
1.5. Proposer un protocole pour préparer cette solution avec le matériel et les éléments de verrerie usuels au laboratoire, dont on précisera le nom et le volume si nécessaire.
Protocole de dissolution :
• Peser précisément m=4,2 g de nitrate d’argent dans une coupelle.
• Prendre une fiole jaugée de 250 mL et introduire à l’aide d’un entonnoir la masse m. (Rincer la coupelle de pesée et l’entonnoir à l’eau distillée en récupérant l’eau du rinçage)
• Remplir la fiole jaugée au ¾ avec de l’eau distillée.
• Boucher la fiole et agiter.
• Ajuster avec de l’eau distillée jusqu’au trait de jauge.
• Agiter. La solution est prête.
2. Modélisation de la transformation chimique intervenant dans l’arbre de Diane
On réalise l’expérience, et on prend en photos le système chimique dans son état initial et dans son état final. Dans l’état initial, la solution est incolore (photographie de gauche ci-après). Après plusieurs heures, la solution se colore progressivement en bleu, et le fil de cuivre se recouvre d’un solide brillant déposé sous forme de « feuillage métallique », qui porte le nom d’«arbre de Diane» (photographie de droite ci-après).


2.1. Justifier qu’une transformation chimique a bien eu lieu.
Nous observons sur les photographies :
Dans l’état initial, la solution est incolore avec un fil de cuivre
Après plusieurs heures, la solution se colore progressivement en bleu (les ions cuivre $Cu^{2+}(aq)$ donnent une couleur bleue aux solutions aqueuses), et le fil de cuivre se recouvre d’un solide brillant.
Le cuivre s’est transformé en ion cuivre $Cu^{2+}(aq)$, un solide brillant recouvre le cuivre. Une transformation chimique a bien eu lieu.
2.2. Identifier les couples mis en jeu lors de la formation d’un arbre de Diane et écrire les deux demi-équations correspondantes.
couple ion argent/argent : $Ag^+/Ag$ ;
couple ion cuivre/cuivre : $Cu^{2+}/Cu$.
$Ag^+(aq)+e^-=Ag(s)$
$Cu(s)=Cu^{2+}(aq)+2e^-$
2.3. En déduire que l’équation de la réaction modélisant la formation de l’arbre de Diane s’écrit :
2Ag+ (aq) + Cu (s) → 2Ag (s) + Cu2+ (aq)
$Ag^+(aq)+e^-=Ag(s)$ ×2
$Cu(s)=Cu^{2+}(aq)+2e^-$
$2Ag^+(aq)+Cu(s)\rightarrow2Ag(s)+Cu^{2+}(aq)$
2.4. Avec la méthode de votre choix, montrer que le cuivre est en excès. La quantité initiale n d’ions argent sera prise égale à 2,2×10-2 mol.
Calculons les quantités initiales des réactifs.
D’après le texte : On souhaite fabriquer un arbre de Diane au laboratoire. Pour ce faire, on place un fil de cuivre, de masse initiale $m’=5,6\ g$
$n_{Cu}^i=\frac{m_{Cu}}{M_{Cu}}=\frac{5,6}{63,5}=8,8.10^{-2}\ mol$
$n_{Ag^+}^i=2,2.10^{-2}\ mol$
Tableau d’avancement :
| Équation | 2Ag+ (aq) | + Cu (s) | 2Ag (s) | + Cu2+ (aq) | |
| État initial | x=0 mol | 2,2.10-2 | 8,8.10-2 | 0 | 0 |
| Etat intermédiaire | x | 2,2.10-2-2x | 8,8.10-2-x | 2x | x |
| Etat final | x=xf | 2,2.10-2-2xf | 8,8.10-2-xf | 2xf | xf |
Calculons $x_{max}$ :
$2,2.10^{-2}-2x_{max1}=0$
$x_{max1}=\frac{2,2.10^{-2}}{2}=1,1.10^{-2}\ mol$
$8,8.10^{-2}-x_{max2}=0$
$x_{max2}=8,8.10^{-2}\ mol$
$x_{max1}<x_{max2}$
$x_{max}=x_{max1}=1,1.10^{-2}\ mol$
2.5. Avec la méthode de votre choix, déterminer la masse d’argent qui se forme sur le fil de cuivre si l’avancement maximal est atteint.
$m_{Ag}=n_{Ag}^f\times M_{Ag}$
si l’avancement maximal est atteint, d’après le tableau d’avancement :
$n_{Ag}^f=2x_{max}$
$m_{Ag}=2x_{max}\times M_{Ag}$
$m_{Ag}=2\times1,1.10^{-2}\times107,9=2,4g$
3. Prévision de l’état final à l’aide d’un script en Python
Le programme suivant, écrit en langage Python, permet de calculer la masse d’argent déposée sur le fil de cuivre.

Ce programme permet aussi de s’assurer que le cuivre est bien introduit en excès : dans le cas contraire, le fil, qui joue aussi le rôle de support, risquerait de casser et l’on perdrait la végétation métallique qui met plusieurs heures à se former.
On exécute le programme. Tout d’abord on indique les conditions expérimentales initiales de l’expérience décrites précédemment. On obtient l’écran suivant :

Écrire la ligne qui apparaîtrait dans la console d’exécution à la suite de la saisie des données initiales ci-dessus. Justifier.
La ligne » La masse d’argent déposée vaut : 2,4 g » apparaît dans la console.
